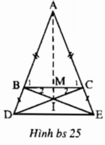
Xét ΔABM và ΔACM có:
AB = AC ( giả thiết)
BM = CM ( vì M là trung điểm BC )
AM chung
⇒ ΔABM = ΔACM (c.c.c)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180o
⇒ ∠AMB = ∠AMC = 90o hay AM ⊥ BC
Chứng minh tương tự ta có: IM ⊥ BC
⇒ A, I, M thẳng hàng (Qua 1 điểm ta kẻ được duy nhất 1 đường thẳng vuông góc với đường thẳng cho trước)
Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D trên tia đối của tia CA lấy điểm E sao cho BD = CE, Gọi I là giao điểm của BE và CD.
a) Chứng minh IB = IC, ID = IE.
b) Chứng minh DE // BC.
c) Gọi M là trung điểm của BC. Chứng minh ba điểm A, M, I thẳng hàng.
Cho tam giác ABC cân tại A . Trên tia đối của tia BA lấy điểm D , trên tia đối của tia CA lấy điểm E sao cho BD=CE. Gọi I là giao điểm của BE và CD .
a) chứng minh rằng IB=IC , ID=IE
b) chứng minh rằng BC//DE
c) Gọi M là trung điểm của BC . Chứng minh rằng ba điểm A , M, I thẳng hàng
Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD.
a) Chứng minh rằng IB = IC, ID = IE.
b) Chứng minh rằng BC // DE.
c) Gọi M là trung điểm của BC. Chứng minh rằng ba điểm A, M, I thẳng hàng.
Cho tam giác ABC cân tại A Trên tia đối của tia BA lấy điểm D Trên tia đối của tia CA lấy điểm E sao cho BD = CE Gọi I là giao điểm của BE và CD
a) Chứng minh rằng IB=IC,ID=IE
b) Chứng minh rằng BC song song với d e
c) Gọi M là trung điểm của BC chứng minh rằng ba điểm A,M,I thẳng hàng
Cho tam giác ABC cân tại A . Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lầy điểm E sao cho BD = CE . Gọi I là giao điểm của BE và CD . Chứng minh:
a) IB = IC , ID = IE
b) BC // DE
c) M là trung điểm BC . Chứng minh A , M , I thẳng hàng
Cho tam giác ABC cân tại A. Trên Tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD. Chứng minh rằng BC song song DE.
Bài 5: Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BA lấy điểm D sao cho DB = BC. Tính số đo các góc của tam giác ACD
Bài6:TamgiácABCcântạiBcóBˆ =100 đôn.LấycácđiểmDvàEtrêncạnhAC sao cho AD = BA, CE = CB. Tính số đo góc DBE?
Bài 7: Cho tam giác ABC cân tại A. Vẽ BH vuông góc với AC tại H. Chứng minh rằng góc BAC có số đo gấp đôi số đo góc CBH.
Bài 8: Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD.
a) Chứng minh tam giác IBC và tam giác IDE là các tam giác cân.
b) Chứng minh BC // DE.
c) Gọi M là trung điểm của BC. Chứng minh ba điểm A, M, I thẳng hàng.
Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. gọi I là giao diểm BE và CD. Chứng minh:
a) IB = IC , ID = IE
b) BC // DE
c) Gọi M là trung điểm của BC. Chứng minh: A, M, I thẳng hàng
Cho tam giác ABC cân tại A. Trên Tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD. Chứng minh rằng IB = IC, ID = IE.
