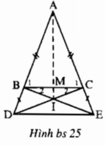
+)Theo giả thiết ta có: AB = AC và BD = CE nên:
AB + BD = AC + CE hay AD = AE.
+) Xét ΔABE và ΔACD có:
AB = AC (gt)
∠A chung
AE = AD (chứng minh trên)
⇒ ΔABE = ΔACD (c.g.c)
⇒ BE = CD (2 cạnh tương ứng) (1)
và ∠ABE = ∠ACD (2 góc tương ứng) (2)
Tam giác ABC cân nên ∠B1 = ∠C1. (3)
Từ (2) và (3) ⇒ ∠ABE - ∠B1 = ∠ACD - ∠C1, tức là ∠B2 = ∠C2.
⇒ ΔBIC cân tại I ⇒ IB = IC. (4)
Từ (1) và (4) suy ra BE - IB = CD – IC, tức là IE = ID.











