
Những câu hỏi liên quan
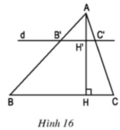
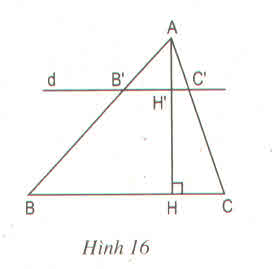
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B, C và H (h.16). a) Chứng minh rằng:
A
H
A
H
B
C
B
C
b) Áp dụng: Cho biết
A...
Đọc tiếp
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H' (h.16).
a) Chứng minh rằng: A H ' A H = B ' C B C
b) Áp dụng: Cho biết A H ' A H = 1 3 và diện tích tam giác ABC là 67,5 cm2. Tính diện tích tam giác AB’C’.
a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒ 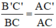
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒ 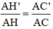
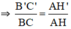
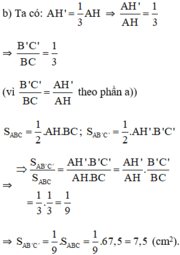
Đúng 0
Bình luận (0)
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B, C và H
a) Chứng minh rằng: .
b) Áp dụng: Cho biết và diện tích tam giác ABC là 67,5 cm2. Tính diện tích tam giác AB’C’.
Đọc tiếp
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H'
a) Chứng minh rằng: 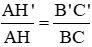
b) Áp dụng: Cho biết 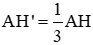
Tam giác ABC có đường cao AH . Đường thẳng d song song với BC , cắt các cạnh AB , AC và đường cao AH theo thứ tự tại các điểm B' , C' và H' .
a) CMR : AH'/AH = B'C'/BC .
b) Cho AH' = 1/3 AH và S tam giác ABC là 67,5 cm2 . Tính S tam giác AB'C' .
a) Ta có : d // BC
=> B'C' // BC
Xét \(\Delta AB'H'\)và \(\Delta ABH\)( B'H' // BH )
Theo hệ quả của định lý Ta-lét
=> \(\frac{AB'}{AB}=\frac{AH'}{AH}\)(1)
Xét \(\Delta AB'C'\) và \(\Delta ABC\)( B'C' // BC )
Theo hệ quả của định lý Ta-lét
=> \(\frac{AB'}{AB}=\frac{B'C'}{BC}\)(2)
Từ (1) và (2)
=> \(\frac{AH'}{AH}=\frac{B'C'}{BC}\)( ĐPCM )
b) \(\frac{SAB'C'}{SABC}=\frac{\frac{1}{2}AH'.B'C'}{\frac{1}{2}AH.BC}=\frac{AH'}{AH}.\frac{B'C'}{BC}=\frac{1}{3}.\frac{1}{3}=\frac{1}{9}\)
=> \(SAB'C'=\frac{1}{9}\Rightarrow SAB'C'=\frac{SABC}{9}=\frac{67,5}{9}=7,5\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B, C và H (h.16)
a) Chứng minh rằng :
dfrac{AH}{AH}dfrac{BC}{BC}
b) Áp dụng : Cho biết AHdfrac{1}{3}AH và diện tích tam giác ABC là 67,5cm^2. Tính diện tích tam giác ABC ?
Đọc tiếp
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H' (h.16)
a) Chứng minh rằng :
\(\dfrac{AH'}{AH}=\dfrac{B'C'}{BC}\)
b) Áp dụng : Cho biết \(AH'=\dfrac{1}{3}AH\) và diện tích tam giác ABC là \(67,5cm^2\). Tính diện tích tam giác AB'C' ?
a) Chứng minh =
Vì B'C' // với BC => = (1)
Trong ∆ABH có BH' // BH => = (2)
Từ 1 và 2 => =
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = AH
= = => B'C' = BC
=> SAB’C’= AH'.B'C' = .AH.
Đúng 1
Bình luận (0)
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường cao AD. Đường thẳng song song với BC, cắt AB,AC và đường cao AD theo thứ tự tại các điểm B',C',D'
a) chứng minh AD'/AD=B'C'/BC
b) Áp dụng: Cho biết AD'=1/3AD và diện tích tam giác ABC là 73,5cm^2. Tính diện tích tam giác AB'C'
a) Ta có: d // BC (gt)
\(\Rightarrow\)B'C' // BC, theo hệ quả của định lí Ta-lét ta có:
\(\frac{AB'}{AB}=\frac{B'C'}{BC}\)(Trong \(\Delta AB'C'\)và \(\Delta ABC\)) (1)
Và \(\frac{AB'}{AB}=\frac{AD'}{AD}\)(Trong \(\Delta AB'D'\)và \(\Delta ABD\)) (2)
Từ (1), (2) \(\Rightarrow\)\(\frac{B'C'}{BC}=\frac{AD'}{AD}\left(3\right)\)
b) Ta có: AD' = \(\frac{1}{3}\)AD (gt) (4) \(\Leftrightarrow\frac{AD'}{AD}=\frac{1}{3}\left(5\right)\)
Từ (3), (5) \(\Rightarrow\frac{B'C'}{BC}=\frac{1}{3}\Leftrightarrow B'C'=\frac{1}{3}BC\)\(\left(6\right)\)
Tích của cạnh đáy BC và đuuờng cao AD là:
\(S_{ABC}=\frac{1}{2}AD.BC\)
\(\Leftrightarrow\)73,5 \(=\frac{1}{2}AD.BC\)
\(\Leftrightarrow\)\(AD.BC=\)73,5 :\(\frac{1}{2}\)
\(\Leftrightarrow\)\(AD.BC=\)147 \(\left(7\right)\)
Diện tích tam giác AB'C' là:
\(S_{AB'C'}=\frac{1}{2}AD'.B'C'\)
Từ (4), (6) \(\Rightarrow S_{AB'C'}\)=\(\frac{1}{2}.(\frac{1}{3}.AD.\frac{1}{3}BC)\)
\(\Leftrightarrow S_{AB'C'}=\frac{1}{2}.\frac{1}{3}.\frac{1}{3}.AD.BC\)
Từ (7) \(\Rightarrow S_{AB'C'}\)\(=\frac{1}{2}.\frac{1}{3}.\frac{1}{3}.147\)
\(=\frac{49}{6}\)
Vậy \(S_{AB'C'}=\frac{49}{6}cm^2\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường cao AH. Vẽ đường thẳng a song song BC cắt AB,AC,AH lần lượt tại M,N,I.
a) Chứng minh AI/AH=MN/BC.
b) Cho AI=1/3 AH . Diện tích ABC = 67,5 cm2. Tính diện tích AMN.
Xem chi tiết
a) Chứng minh =
Vì B’C’ // với BC => = (1)
Trong ∆ABH có BH’ // BH => = (2)
Từ 1 và 2 => =
b) B’C’ // BC mà AH ⊥ BC nên AH’ ⊥ B’C’ hay AH’ là đường cao của tam giác AB’C’.
Áp dụng kết quả câu a) ta có: AH’ = AH
= = => B’C’ = BC
=> SAB’C’= AH’.B’C’ = .AH.BC
=>SAB’C’= (AH.BC)
mà SABC= AH.BC = 67,5 cm2
Vậy SAB’C’= .67,5= 7,5 cm2
Cho tam giác ABC có đường cao AH trọng tâm G. Một đường thẳng đi qua G và song song với BC cắt các cạnh AB, AC tại M và N. Nếu diện tích tam giác ABC bằng 36 cm2 thì diện tích tam giác HMN bằng ... cm2
Cho tam giác ABC nhọn, đường cao AH. Lấy điểm I bất kỳ trên cạnh AH. Qua I kẻ đường
thẳng song song với BC, cắt AB, AC lần lượt tại D, E.
a) Chứng minh: AI/AH=DE/BC
b) Cho
AI/AH=1/4
và diện tích tam giác ADE là 10 cm2
. Tính diện tích tam giác ABC.
Cho tam giác ABC có cạnh BC = 40cm, đường cao AH = 16cm, trên cạnh AH lấy điểm M là điểm chính giữa, kẻ qua M đường thẳng song song với BC cắt AB và AC lần lượt tại E và F. Nối C với E
a.Tính diện tích tam giác ABC
b.Tính diện tích tam giác BEC
Bạn ơi! Bạn vẽ hình đi nha! Mik đọc thấy khó hiểu quá
Đúng 0
Bình luận (0)

















