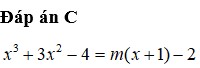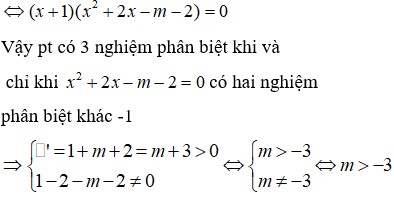cho hàm số y=f(x)=(x+4)|x+2| tìm m để hàm số y=f(x) cắt đường thẳng y=m tại 3 điểm phân biệt

Những câu hỏi liên quan
Cho hàm số Y=f(x) = \(y=\frac{x-1}{2x-3}\) Tìm xác định hàm số f(x) và tính f(1) ,f(2). Xác định m để đường thẳng y =x-m cắt P tại 2 điểm pân biệt
Cho hàm số yf(x) xác định và liên tục trên các khoảng
(
-
∞
;
0
)
,
(
0
;
+
∞
)
và có bảng biến thiên như sauTìm tất cả các giá trị thực của m để đường thẳng ym cắt đổ thị hàm số yf(x) tại 3 điểm phân biệt A.
-
4
≤
m
0
B.
-
4
m
0...
Đọc tiếp
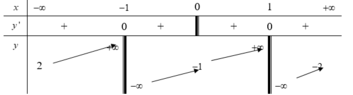
Cho hàm số y=f(x) xác định và liên tục trên các khoảng ( - ∞ ; 0 ) , ( 0 ; + ∞ ) và có bảng biến thiên như sau
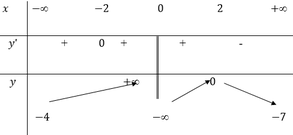
Tìm tất cả các giá trị thực của m để đường thẳng y=m cắt đổ thị hàm số y=f(x) tại 3 điểm phân biệt
A. - 4 ≤ m < 0
B. - 4 < m < 0
C. - 7 < m < 0
D. - 4 < m ≤ 0
Cho đồ thị hàm số y f(x) như hình vẽ bên. Giá trị m để đường thẳng y 2m cắt đồ thị hàm số
y
f
x
tại 4 điểm phân biệt là A.
−
2
m
2
B.
−
1
≤
m
≤
1
C. ...
Đọc tiếp
Cho đồ thị hàm số y = f(x) như hình vẽ bên. Giá trị m để đường thẳng y = 2m cắt đồ thị hàm số y = f x tại 4 điểm phân biệt là
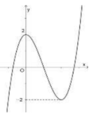
A. − 2 < m < 2
B. − 1 ≤ m ≤ 1
C. − 1 < m < 1
D. m = 1
Đáp án C.
Đồ thị hàm số y = f x C 1 được suy ra từ đồ thị của hàm số y = f x C như sau:
+ Hàm số y = f x là hàm chẵn có đồ thị đối xứng qua trục tung
+ Hàm số y = f x = f x , x ≥ 0 − f x , x < 0
+ Đồ thị hàm số y = f x gồm hai phần
Phần 1: Là đồ thị (C) ở bên phải trục Oy
Phần 2: Đối xứng của phần 1 qua Oy
+ Vẽ đồ thị C 1 như hình vẽ
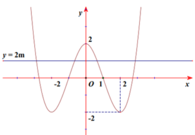
Để đường thẳng y = 2m cắt C 1 tại 4 điểm phân biệt khi − 2 < 2 m < 2 ⇔ − 1 < m < 1
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có bảng biến thiên sauTất cả các giá trị thực của tham số m để đường thẳng y1-m cắt đồ thị hàm số đã cho tại hai điểm phân biệt là: A. m-2 hoặc m2 B.
m
≥
2
C.
m
≤
-
1
hoặc
m
≥
2
D. m-1 hoặc m3
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên sau
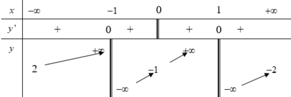
Tất cả các giá trị thực của tham số m để đường thẳng y=1-m cắt đồ thị hàm số đã cho tại hai điểm phân biệt là:
A. m<-2 hoặc m>2
B. m ≥ 2
C. m ≤ - 1 hoặc m ≥ 2
D. m<-1 hoặc m>3
, Cho hàm số yx-1/x^2+mx+4. Tìm m để đồ thị hàm số có 2 đường tiện cận
13, tìm m để(C):y mx^3-x^2-2x+8m cắt Ox tại 3 điểm phân biệt có Hoành độ âm
14,cho (C) :y x^3+(m+2) x+1 d:y 2x-1 Tìm m để d cắt C tại 1 điểm duy nhất có Hoành độ dương
15, tìm m để phương trình -x^4+2x^2+3x+2m0 có 3 nghiệm phân biệt
Đọc tiếp
, Cho hàm số y=x-1/x^2+mx+4. Tìm m để đồ thị hàm số có 2 đường tiện cận 13, tìm m để(C):y= mx^3-x^2-2x+8m cắt Ox tại 3 điểm phân biệt có Hoành độ âm 14,cho (C) :y= x^3+(m+2) x+1 d:y= 2x-1 Tìm m để d cắt C tại 1 điểm duy nhất có Hoành độ dương 15, tìm m để phương trình -x^4+2x^2+3x+2m=0 có 3 nghiệm phân biệt
1) cho hàm số y=2x+b. Tìm b để hàm số cắt trục hoành tại điểm có hoành độ bằng 3.
2) Cho Parabol (P): y=x2 và đường thẳng d: y=(m-1)x+m-4. Tìm m để d cắt (P) tại 2 điểm phân biệt nằm về 2 phía của trục tung.
1, Do hàm số trên cắt trục hoành tại điểm có hoành độ bằng 3 hay hàm số trên đi qua A(3;0)
<=> \(0=6+b\Leftrightarrow b=-6\)
2, Hoành độ giao điểm (P) ; (d) tm pt
\(x^2-\left(m-1\right)x-m+4=0\)
Để (P) cắt (d) tại 2 điểm pb nằm về 2 phía trục tung khi pt có 2 nghiệm trái dấu hay
\(x_1x_2=-m+4< 0\Leftrightarrow-m< -4\Leftrightarrow m>4\)
1) Cho hàm số: yx^2-3x+4 có đồ thị là P và đường thẳng d có phương trình:y2x-m, và m là tham số. Tìm các giá trị của m để d cắt P tại hai điểm phân biệt A,B sao cho: OA^2+OB^257 và khi đó O là toa độ góc2) Cho hàm số fleft(xright)sqrt{3-x}-sqrt{3+x}-x^3-x. Tìm tất cả giá trị của tham số a để tập nghiệm của bất phương trình fleft(2x-1right)fleft(-2aright) có ít nhất là 3 số nguyên
Đọc tiếp
1) Cho hàm số: \(y=x^2-3x+4\) có đồ thị là P và đường thẳng d có phương trình:
\(y=2x-m\), và m là tham số. Tìm các giá trị của m để d cắt P tại hai điểm phân biệt \(A,B\) sao cho: \(OA^2+OB^2=57\) và khi đó O là toa độ góc
2) Cho hàm số \(f\left(x\right)=\sqrt{3-x}-\sqrt{3+x}-x^3-x\). Tìm tất cả giá trị của tham số a để tập nghiệm của bất phương trình \(f\left(2x-1\right)>f\left(-2a\right)\) có ít nhất là 3 số nguyên
Tìm m để đường thẳng y=m(x+1)-2 cắt đồ thị hàm số y = x 3 + 3 x 2 - 4 tại ba điểm phân biệt
A. m>3
B. m<3
C. m>-3
D. m<-3
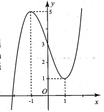
Cho hàm số yf(x) liên tục trên R, có đồ thị (C) như hình bên. Tìm tất cả các giá trị thực của tham số m để đường thẳng y2m-1 cắt đồ thị (C) tại 2 điểm phân biệt A. B. C. D.
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R, có đồ thị (C) như hình bên. Tìm tất cả các giá trị thực của tham số m để đường thẳng y=2m-1 cắt đồ thị (C) tại 2 điểm phân biệt
A.![]()
B. ![]()
C. ![]()
D. ![]()