Hãy xác định bài toán và viết thuật toán bằng cách liệt kê để giải bài toán tìm kiếm tuần tự khoá K trong một dãy số a1, a2,....,aN.
Các bước thuật toán viết trên từng dòng là!
#include <bits/stdc++.h>
using namespace std;
long long a[10000],n,i,k,vt;
int main()
{
cin>>n>>k;
for (i=1; i<=n; i++)
cin>>a[i];
vt=0;
for (i=1; i<=n; i++)
if (a[i]==k) vt=i;
cout<<vt;
return 0;
}
Đúng 0
Bình luận (0)
hãy xác định bài toán và viết thuật toán bằng cách liệt kê để giải bài toán sau đây: tính giá trị S
biết S có công thức:
S = 3xy + 2x - 3y ( x,y là số thực )
#include <bits/stdc++.h>
using namespace std;
double x,y;
int main()
{
cin>>x>>y;
cout<<3*x*y+2*x-3*y;
return 0;
}
Đúng 2
Bình luận (1)
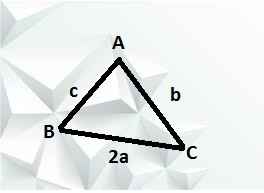 cho hình tam giác ABC và độ dài ba cạnh của tam giác như hình vẽ . tính chu vi của tam giác ABC
cho hình tam giác ABC và độ dài ba cạnh của tam giác như hình vẽ . tính chu vi của tam giác ABC
a , hãy xaxc định đầu vào ( INPUT ) VÀ ĐẦU RA ( OUTPUT ) của bài toán
b, viết thuật toán mô tả các bước giải bài tonas trên
a: Input: a,b,c
Output: a+b+c
b: Bước 1: Nhập a,b,c
Bước 2: Xuất a+b+c
Bước 3: kết thúc
Đúng 2
Bình luận (0)
Bài 1: viết các biểu thức toán sau đây dưới dạng biểu thức Pascal (viết dưới dạng chương trình)
a/left(5-1right)^2chia cho 3 lấy dư
b/10^2+dfrac{24-4}{4}
Bài 2: Em hãy xác định bài toán và mô tả thuật toán cho bài toán sau: tính diện tích và chu vi của một thửa ruộng hình chữ nhật có chiều dài là b, chiều rộng là a
Đọc tiếp
Bài 1: viết các biểu thức toán sau đây dưới dạng biểu thức Pascal (viết dưới dạng chương trình)
a/\(\left(5-1\right)^2\)chia cho 3 lấy dư
b/\(10^2+\dfrac{24-4}{4}\)
Bài 2: Em hãy xác định bài toán và mô tả thuật toán cho bài toán sau: tính diện tích và chu vi của một thửa ruộng hình chữ nhật có chiều dài là b, chiều rộng là a
Bai1: a) \(sqr\left(5-1\right)\) mod 3
b) \(sqr\left(10\right)+\left(25-4\right)\)/4
Bai2:Xác định bải toán
Input : Chiều dài b và chiều rộng a.
Output: Diện tích và chu vi thửa ruộng.
Thuật toán
B1:Nhập a,b
B2:CV<-- (a+b)*2
Và S<--a*b
B3: -Thông báo lên màn hình diện tích là s
-Và chu vi là cv
Đúng 0
Bình luận (0)
Chỉ ra cách trình bày (kênh chữ, kênh hình) và cách triển khai ý tưởng, thông tin trong văn bản Nước biển dâng: bài toán khó cần giải trong thế kỉ XXI. Phân tích hiệu quả của cách trình bày và triển khai ấy.
- Cách trình bày (kênh chữ, kênh hình) và cách triển khai ý tưởng, thông tin trong văn bản: văn bản triển khai theo trình từ mức độ quan trọng của hiện tượng, giúp truyền tải thông tin đến người đọc một cách rõ ràng, cụ thể và chính xác.
- Tính hiệu quả của cách trình bày và triển khai ấy: giúp người đọc nắm bắt được những dữ liệu quan trọng về hiện tượng này theo trình tự hợp lí, đầy logic.
Đúng 1
Bình luận (0)
Tính trung bình cộng của a số a , b, c . Hãy tìm Input và Output và mô tả thuật toán cho bài .
Input: a,b,c
Output: (a+b+c)/3
Đúng 1
Bình luận (1)
Mô tả thuật toán của các bài toán sau:
a/ tìm giá trị tuyệt đối của một số a cho trước
b/ tìm số lớn nhất trong ba số a, b và c nhập từ bàn phím
program bai_5;
uses crt;
var a,b,c :real;
BEGIN
write('nhap vao so a'); Readln(a);
write('nhap vao so b'); Readln(b);
write('nhap vao so c'); Readln(c);
if a<0 then a:=-a;
max:=a;
if max <b then max:=b;
if max<c then max:=c;
write('gia tri tuyet doi cua a la:',a);
write('so lon nhat trong ba so a,b,c la:',max);
Readln
END.
Thanks
Đúng 0
Bình luận (1)
Xét bài toán: Cho một điểm M nằm bên trong góc xOy sao cho khoảng cách từ M đến hai cạnh Ox, Oy bằng nhau. Chứng tỏ rằng OM là tia phân giác của góc xOyHãy sắp xếp một cách hợp lý các câu sau để được lời giải của bài toán trên.a. Do đó ΔOMAΔOMBb.Gọi MA và MB theo thứ tự là khoảng cách từ M đến Ox và Oyc. Xét hai tam giác vuông OMA và OMB có:OM là cạnh chungMA MB (gt)d. Suy ra:
M
O
A...
Đọc tiếp
Xét bài toán: "Cho một điểm M nằm bên trong góc xOy sao cho khoảng cách từ M đến hai cạnh Ox, Oy bằng nhau. Chứng tỏ rằng OM là tia phân giác của góc xOy"
Hãy sắp xếp một cách hợp lý các câu sau để được lời giải của bài toán trên.
a. Do đó ΔOMA=ΔOMB
b.Gọi MA và MB theo thứ tự là khoảng cách từ M đến Ox và Oy
c. Xét hai tam giác vuông OMA và OMB có:
OM là cạnh chung
MA = MB (gt)
d. Suy ra: M O A ^ = M O B ^ (hai góc tương ứng)
e.Vậy OM là tia phân giác của x O y ^
Sắp xếp nào sau đây đúng:
A. b, c, a, d, e
B. b, a, d, c, e
C. b, c, d, a, e
D. c, b, a, d, e
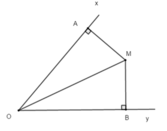
Gọi MA và MB theo thứ tự là khoảng cách từ M đến Ox và Oy
Xét hai tam giác vuông OMA và OMB có:
OM là cạnh chung
MA = MB (gt)
Do đó ΔOMA=ΔOMB (cạnh huyền – cạnh góc vuông)
Suy ra: M O A ^ = M O B ^ (hai góc tương ứng)
Vậy OM là tia phân giác của x O y ^
Vậy thứ tự sắp xếp phải là: b, c, a, d, e.
Chọn đáp án A
Đúng 0
Bình luận (0)
Tổng hs lớp 9A và 9B là 62. Điểm thi môn toán học kì I của hai lớp được ghi lại như sau : tổng điểm thi của hai lớp là 394 điểm, điểm thi trung bình của lớp 9A là 6,5 ,điểm thi trung bình của lớp 9B là 6,2. Tính số học sinh lớp 9A và 9B.( giải bài toán bằng cách lập hệ pt )
Cho hình chữ nhật ABCD và hình bình hành AMCN có các kính thước ghi trên hình vẽ . Tính diện tích của hình bình hành AMCN bằng hai cách khác nhau (vở bài tập toán lớp 5 , tập 1 , trang 110)
GIẢI:
Nối hai điểm AC ta được 2 hình tam giác ACN và ACM có diện tích bằng nhau (vì có độ dài đáy bằng nhau AM = CN = 14 cm và chiều cao bằng nhau AD = BC = 18 cm).
Diện tích hình tam giác ACN là:
14 x 8 : 2 = 56 (cm2)
Ta có: Diện tích hình bình hành AMCN = diện tích hình tam giác ACN = diện tích hình tam giác ACM.
Diện tích hình bình hành AMCN là:
56 x 2 = 112 (cm2)
Đáp số: 112 cm2.
(tick giúp với ạ)
Đúng 2
Bình luận (0)




















