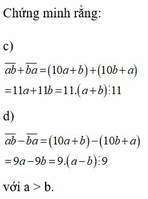Tại sao ab+ba chia hết cho 11

Những câu hỏi liên quan
chứng minh tại sao (ab+ba) chia hết cho 11
ab + ba = 10 x a + b + 10 x b + a
= a x (10 +1) + b x (10 + 1)
= a x 11 + b x 11
= 11 x (a+b)
=> Tổng chia hết cho 11
Đúng 0
Bình luận (0)
tìm ab - ba sao cho ab - ba chia hết cho 11
ab-ba
= ( 10 a + b ) - ( 10 b + a )
= 9a -9b
= 9(a-b) \(⋮\)11
mà \(ƯCLN\left(9;11\right)=1\)=> a-b \(⋮\)11
mà a - b \(\le\)9
do đó a-b = 0
=> a=b
=> ...
Đúng 0
Bình luận (0)
Chứng tỏ rằng
a) ab+ba chia hết cho 11
b) ab–ba chia hết cho 9
c) abba chia hết cho 11
Xem chi tiết
a/ \(\overline{ab}+\overline{ba}=10a+b+10b+a=11a+11b=11\left(a+b\right)⋮11\)
b/ \(\overline{ab}-\overline{ba}=10a+b-10b-a=9a-9b=9\left(a-b\right)⋮9\)
c/ \(\overline{abba}=1001a+110b=11.91.a+11.10.b=11\left(91a+10b\right)⋮11\)
cho ab+ba(có gạch trên đầu)chia hết cho 11. CM ab-ba chia hết cho 11
có: \(\overline{ab}\) + \(\overline{ba}\)
= 10a + 1b + 10b + 1a
= (10a + 1a) + (10b + 1b)
= 11a + 11b = 11.(a+b) \(⋮11\)
Vậy với mọi số tự nhiên a và b thì \(\overline{ab}\)+ \(\overline{ba}\) luôn chia hết cho 11
Đúng 0
Bình luận (0)
CMD : a) abccba chia hết cho 11
b) ab + ba chia hết cho 11
c) ab - ba chia hết cho 9
giúp vs mai nộp r
a) abccba = a.100000 + b + 10000 + c.1000 + c.100 + b .10 + a
= (100000 + 10000 + 1000 + 100 + 10 + 1) (a + b + c + c + b + a)
= 111111 (a + b + c + c + b + a)
= 10101 . 11 (a + b + c + c + b + a)
=> chia hết cho 11
b) Ta có : ab + ba
= 10a + b + 10b + a
= 11a + 11b
Ta có 11a chia hết cho 11; 11b chia hết cho 11
=> ab + ba chia hết cho 11
c) ab - ba
= 10a + b - 10 + a
= 9a + 9b
Ta có 9a chia hết cho 9;9b chia hết cho 9
=> ab - ba chia hết cho 9
Đúng 0
Bình luận (0)
Chứng minh rằng:
a) a b ¯ + b a ¯ chia hết cho 11.
b) a b ¯ - b a ¯ chia hết cho 9 với a > b.
a)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
b)ab-ba⋮9
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b-10b+a
= 9a - 9b
Ta thấy: 9a⋮9 ; 9b⋮9
=>ab+ba⋮9 (ĐPCM)
Đúng 2
Bình luận (0)
Chứng minh rằng:
a, a b + b a chia hết cho 11
b, a b - b a chia hết cho 9 với a > b
a, a b + b a = (10a+b)+(10b+a) = 11a+11b = 11.(a+b) ⋮ 11
b, a b - b a = (10a+b) - (10b+a) = 9a - 9b = 9(a - b) ⋮ 9 (a>b)
Đúng 0
Bình luận (0)
Chứng minh rằng :
a) abccba chia hết cho 11; b) ab + ba chia hết cho 11
c) Nếu abc + def chia hết cho 37 => abcdef chia hết cho 37
d) Nếu ab + cd + ef chia hết cho 11 => abcdef chia hết cho 11
b.ab+ba chia hết cho 11
=>10a+b + 10b+a chia hết cho 11
=>10a+a + 10b+b chia hết cho 11
=>11a+11b chia hết cho 11(đfcm)
Đúng 0
Bình luận (0)
Chứng tỏ rằng:
a)ab-ba chia hết cho 9
b)Nếu ab + cd chia hết cho 11 thì abcd chia hết cho 11
a) ab - ba = a .10+b - (b .10+a)
= a .10+b - b .10 - a
=( a .10 - a)-(b.10-b)
= a.9-b.9
= 9.(a-b) chia het cho 9
b) abcd = ab .100 +cd
= ab .99 +ab+cd
= ab .11 . 9 +(ab+cd)
vì ab .11 .9 chia hết cho 11 nên nếu ab+cd chia hết cho 11 thì abcd chia hết cho 11
Đúng 0
Bình luận (0)
b)Ta có:abcd=ab.100+cd
=ab.99+ab+cd
=ab.11.99+(ab+cd)
Vì 11\(⋮\)11=>ab.11.9 chia hết cho 11
=>(ab+cd)chia hết cho 11
Vậy abcd chia hết cho 11
k mik nha
Đúng 0
Bình luận (0)