
Những câu hỏi liên quan
Cho tam giác ABC cân tại A có AB 10cm, BH 6cm. Vẽ AH vuông góc BC tại H. a, Tính AH ?b) Chứng minh tam giác ABH tam giác ACH , từ đó chứng minh AH là tia phân giác của góc A. c) Từ H vẽ HM vuông góc AB (M ϵ AB) và kẻ HN vuông góc AC (N ϵ AC) . Chứng minh : tam giác BHM tam giác HCN d) Từ B kẻ Bx vuông góc AB, từ C kẻ Cy vuông góc AC chúng cắt nhau tại O. Tam giác OBC là tam giác gì? Vì sao? CÁC BẠN VẼ HÌNH GIÚP MÌNH NHA! MÌNH CẢM ƠN CÁC BẠN!
Đọc tiếp
Cho tam giác ABC cân tại A có AB = 10cm, BH = 6cm. Vẽ AH vuông góc BC tại H.
a, Tính AH =?
b) Chứng minh tam giác ABH= tam giác ACH , từ đó chứng minh AH là tia phân giác của góc A.
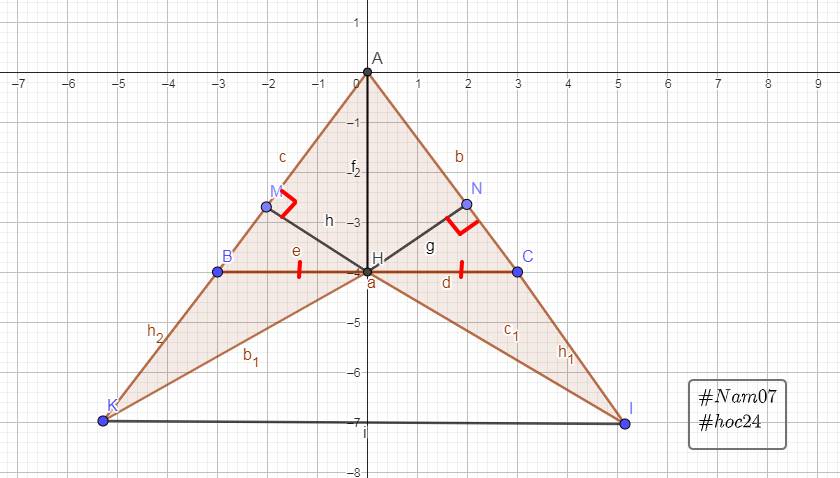
c) Từ H vẽ HM vuông góc AB (M ϵ AB) và kẻ HN vuông góc AC (N ϵ AC) .
Chứng minh : tam giác BHM = tam giác HCN
d) Từ B kẻ Bx vuông góc AB, từ C kẻ Cy vuông góc AC chúng cắt nhau tại O. Tam giác OBC là tam giác gì? Vì sao?
CÁC BẠN VẼ HÌNH GIÚP MÌNH NHA! MÌNH CẢM ƠN CÁC BẠN! ![]()
a: Ta có: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=10^2-6^2=64\)
=>\(AH=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
c: Ta có: ΔAHB=ΔAHC
=>BH=CH
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
d: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>ΔOBC cân tại O
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC =10cm, BC = 12cm. Vẽ AH vuông góc BC tại H. a) Chứng minh: ABC cân. (1đ) b) Chứng minh = AHB AHC , từ đó chứng minh AH là tia phân giác của góc A. (2đ) c) Từ H vẽ HM ⊥ AB ( ) M AB và kẻ HN ⊥ AC ( ) N AC . Chứng minh : BHM = HCN (1,5đ) d) Tính độ dài AH. (1đ) e) Từ B kẻ Bx ⊥ AB, từ C kẻ Cy ⊥ AC chúng cắt nhau tại O. Tam giác OBC là tam giác gì? Vì sao? (1đ)
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H
a/ Chứng minh :tam giác AHB tam giác AHCvà AH là tia phân giác của góc BAC
b/ Từ H kẻ HM vuông góc với AB, HN vuông góc với AC ,AH cắt MN tại K. Chứng minh AH vuông góc với MN
c/ Trên tia đối của tia HM lấy P sao cho H là trung điểm của MP, NP cắt BC tại E, NH cắt ME tại Q. Chứng minh: P, Q, K thẳng hàng.
Đọc tiếp
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H
a/ Chứng minh :tam giác AHB = tam giác AHCvà AH là tia phân giác của góc BAC
b/ Từ H kẻ HM vuông góc với AB, HN vuông góc với AC ,AH cắt MN tại K. Chứng minh AH vuông góc với MN
c/ Trên tia đối của tia HM lấy P sao cho H là trung điểm của MP, NP cắt BC tại E, NH cắt ME tại Q. Chứng minh: P, Q, K thẳng hàng.
1.Cho tam giác ABC có AB3cm,AC4cm,BC5cma) Chứng tỏ tam giác ABC vuông tại A.b) Trên tia đối của tia AC lấy điểm D sao cho CD6cm.Tính độ dài đoạn thẳng BD.2.Cho tam giác ABC, biết AB 12cm,AC 9cm,BC 15cm.a) Chứng tỏ tam giác ABC vuông.b) Kẻ AH vuông góc với BC tại H, biết AH 7,2cm.Tính độ dài đoạn thẳng BH và HC.3.Cho tam giác nhọn ABC(ABAC). Kẻ AH vuông góc với BC tại H. Tính chu vi tam giác ABC biết AC 20cm, AH 12cm, BH 5cm.4.Cho tam giác ABC cân tại A, kẻ AH vuông góc với BCa) Chứng minh...
Đọc tiếp
1.Cho tam giác ABC có AB=3cm,AC=4cm,BC=5cm
a) Chứng tỏ tam giác ABC vuông tại A.
b) Trên tia đối của tia AC lấy điểm D sao cho CD=6cm.Tính độ dài đoạn thẳng BD.
2.Cho tam giác ABC, biết AB = 12cm,AC = 9cm,BC = 15cm.
a) Chứng tỏ tam giác ABC vuông.
b) Kẻ AH vuông góc với BC tại H, biết AH = 7,2cm.Tính độ dài đoạn thẳng BH và HC.
3.Cho tam giác nhọn ABC(AB<AC). Kẻ AH vuông góc với BC tại H. Tính chu vi tam giác ABC biết AC = 20cm, AH = 12cm, BH = 5cm.
4.Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC
a) Chứng minh tam giác AHB = tam giác AHC
b) Từ H kẻ HM vuông góc với AB tại M. Trên cạnh AC lấy điểm N sao cho BM = CN. Chứng minh HN vuông góc AC.
5.Cho tam giác ABC cân tại A, tia phân giác của góc A cắt BC tại I
a) Chứng minh tam giác AIB = tam giác AIC
b) Lấy M là trung điểm AC. Trên tia đối của tia MB lấy điểm D sao cho MB = MD. Chứng minh AD song song BC và AI vuông góc AD.
c) Vẽ AH vuông góc BD tại H, vẽ CK vuông góc BD tại K. Chứng minh BH = DK.
6.Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc BD(E thuộc BD). AE cắt BC ở K.
a) Chứng minh tam giác ABE = tam giác KBE và suy ra tam giác BAK cân.
b) Chứng minh tam giác ABD = tam giác KBD và DK vuông góc BC.
c) Kẻ AH vuông góc BC(H thuộc BC). Chứng minh AK là tia phân giác của HAC.
Mọi người vẽ hình lun 6 bài giúp mình nha! Mình đang cần gấp!:(
Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
a) Áp dụng định lý Pytago vào \(\Delta\)ABC có
AB2+AC2=BC2
thay AB=3cm, AC=4cm va BC=5cm, ta có:
32+42=52
=> 9+16=25 (luôn đúng)
=> đpcm
b) có D nằm trên tia đối của tia AC
=> D,A,C thằng hàng và A nằm giữa D và C
=> DA+AC=DC
=> DA+4=6
=>DA=2(cm)
áp dụng định lý Pytago vào tam giác ABD vuông tại A có:
AB2+AD2=BD2
=> 32+22=BD2
=> 9+4=BD2
=> \(BD=\sqrt{13}\)(cm)
Xem thêm câu trả lời
cho tam giác ABC cân tại A ( góc A < 90 độ ) vẽ AH vuông góc BC tại H
a) c/m tam giác AHC = tam giác AHB
b) kẻ HM vuông góc AC tai H . Trên tia đối của tia HM lấy N sao cho HN = HM . Chứng minh BN // AC
c) kẻ HQ vuông góc AB tại Q . C/m BC là trung trực của NQ
a/ Xét tam giác AHB và tam giác AHC có:
AB = AC (vì tam giác ABC cân tại A)
góc ABC = góc ACB (vì tam giác ABC cân tại A)
AH: cạnh chung
=> tam giác AHB = tam giác AHC (c.g.c)
Đúng 0
Bình luận (0)
tam giác ABC cân tại A,H là trung điểm của BC
a.Chứng minh tam giác ABH =tam giác AHC và AH vuông góc với BC
b,kẻ HM vuông góc với AC tại M, kẻ HN vuông góc với AC tại N.Chứng minh tam giác AHM=Tam giác AHN
c. Gọi I là giao điểm của MH và AC,K là giao điểm của NH và AB. Chứng minh tam giác AIK là tam giác cân
`#3107.101107`
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.
Đúng 1
Bình luận (0)
Cho tam giác ABC có ABAC10cm, BC 12 . Vẽ AH vuông góc với BC tại H.a, CMR: tam giác ABC cânb, Chứng minh tam giác AHB tam giác AHC. Từ đó chứng minh AH là phân giác của góc Ac, Từ H vẽ HN vuông góc với Ab và kẻ HN vuông góc với Ac. CMR : tam giác BHM tam giác CHNe, Tính độ dài AHf, Từ B kẻ Bx vuông góc với AB, từ C kẻ Cy vuông góc với AC, chúng cắt nhau tại O. Tam giác OBC là tam giác gì ? Vì sao ?
Đọc tiếp
Cho tam giác ABC có AB=AC=10cm, BC= 12 . Vẽ AH vuông góc với BC tại H.
a, CMR: tam giác ABC cân
b, Chứng minh tam giác AHB = tam giác AHC. Từ đó chứng minh AH là phân giác của góc A
c, Từ H vẽ HN vuông góc với Ab và kẻ HN vuông góc với Ac. CMR : tam giác BHM = tam giác CHN
e, Tính độ dài AH
f, Từ B kẻ Bx vuông góc với AB, từ C kẻ Cy vuông góc với AC, chúng cắt nhau tại O. Tam giác OBC là tam giác gì ? Vì sao ?
a) Vì AB = AC =10cm => (đpcm)
b) Xét \(\Delta AHB\)và \(\Delta AHC\)có;
AB = AC(gt)
\(\widehat{AHB}=\widehat{AHC}=90^o\)
AH chung
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)\)
\(\Rightarrow HB=HC\)(2 cạnh tương ứng)(1)
\(\Rightarrow\widehat{B}=\widehat{C}\)(2 góc tương ứng)(2)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\Rightarrow\)AH là tia phân giác của \(\widehat{A}\)
c) HM với HN?
Vì \(\Delta HMB;\Delta HNC\)là tam giác vuông nên từ (1);(2) =>\(\Delta HMB=\Delta HNC\)
e)Xét \(\Delta AHC\)vuông:
Áp dụng định lí Py ta go ta có:
\(AC^2=CH^2+AH^2\)
\(12^2=6^2+AH^2\)
\(\Rightarrow AH^2=12^2-6^2=144-36=108\)
\(\Rightarrow AH=\sqrt{108}cm\)
Thông cảm nhé tối qua mình tắt mất nên nay làm tiếp:D
Vì \(\widehat{ABO}=\widehat{ACO}=90^o\)mà \(\widehat{ABC}=\widehat{ACB}=60^o\Rightarrow\widehat{BCO}=\widehat{CBO}=30^o\)
Do \(\widehat{BCO}=\widehat{CBO}=30^o\)nên \(\Delta OBC\)là tam giác cân
Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ AH vuông góc với BC tại H.
a) Chứng minh: △ABC cân
b) Chứng minh: △AHB = △AHC, từ đó chứng minh AH là tia phân giác của góc A
c) Từ H vẽ HM ⊥ AB (M ϵ AB) và kẻ HN ⊥ AC (N ϵ AC). Chứng minh: △BHM = △HCN
d) Tính độ dài AH
â)Ta có : AB = AC =10 cm (gt)
=> tam giác ABC cân tại A (2 cạnh bên = nhau )
b) Xét tam giác AHB va tam giac AHC ,co :
\(\widehat{AHB}=\widehat{AHC}=90^O\) ( AH là đường cao )
AB =AC =10 cm (gt )
AH là cạnh chung
Do đo : tam giác AHB =tam giác AHC ( cạnh huyền - cạnh góc vuông )
=>\(\widehat{BAH}=\widehat{CAH}\)( hai góc tương ứng )
=>AH là tia phân giác của góc A
c)Vì trong tam giác cân đường phân giác đồng thời là đường trung tuyến của tam giác
Nên :H là trung điểm của BC
=>BH = CH = \(\frac{BC}{2}\)=12/2 = 6 cm
Đúng 0
Bình luận (0)
TRẢ LỜI TIẾP CÂU Ở TRÊN NHA ( HỒI NÃY BẤM NHẦM GỬI TRẢ LỜI )
b) Vì trong tam giác cân đường phân giác đồng thời là đường trung tuyến của tam giác
Nên : H là trung điểm của BC
=> BH =CH =\(\frac{BC}{2}=\frac{12}{2}=6cm\)
Xét : tam giác BMH và tam giác HCN , co :
BH = CH = 6cm ( chứng minh trên )
\(\widehat{M}=\widehat{N}=90^o\left(gt\right)\)
\(\widehat{B}=\widehat{C}\) (Vì tam giác ABC cân tại A nên hai góc ở đáy = nhau )
Do do:tm giác BHM = tam giác HCN
đ) Áp dụng định lý pytago vào tam giác AHC vuông tại H
\(AH^2=AC^2-HC^2\) =\(10^2-6^2\)=\(100-36=64\)
=>\(AH=\sqrt{64}=8cm\) OK CHÚC BẠN HỌC TỐT
Đúng 0
Bình luận (0)
1.a)
Vì AB=AC => Tam giác ABC cân
b)
Vì △ABC cân
=> góc ABC=góc ACB (1)
góc AHC=góc AHB=90 độ (2)
AB=AC (gt) (3)
Từ (1)(2)(3) => △AHB = △AHC (cạnh huyền-góc nhọn)
=> góc BAH = góc CAH
=> AH là tia phân giác của góc A
c) Vì góc ABC = góc ACB
=> góc MBH = góc NCH
góc BMH = góc HNC =90 độ
=> △BHM = △HCN (g.g)
d) Ta có: AH.BC=AB.AC
=> AH.12=10.10
=> AH = 25/3 (cm)
Xem thêm câu trả lời
Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ AH vuông góc với BC tại H.
a) Chứng minh: △ABC cân
b) Chứng minh: △AHB = △AHC, từ đó chứng minh AH là tia phân giác của góc A
c) Từ H vẽ HM ⊥ AB (M ϵ AB) và kẻ HN ⊥ AC (N ϵ AC). Chứng minh: △BHM = △HCN
d) Tính độ dài AH
Bạn ơi có gải ko đăng lên đi
1.a)
Vì AB=AC => Tam giác ABC cân
b)
Vì △ABC cân
=> góc ABC=góc ACB (1)
góc AHC=góc AHB=90 độ (2)
AB=AC (gt) (3)
Từ (1)(2)(3) => △AHB = △AHC (cạnh huyền-góc nhọn)
=> góc BAH = góc CAH
=> AH là tia phân giác của góc A
c) Vì góc ABC = góc ACB
=> góc MBH = góc NCH
góc BMH = góc HNC =90 độ
=> △BHM = △HCN (g.g)
d) Ta có: AH.BC=AB.AC
=> AH.12=10.10
=> AH = 25/3 (cm)





















