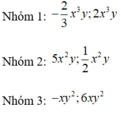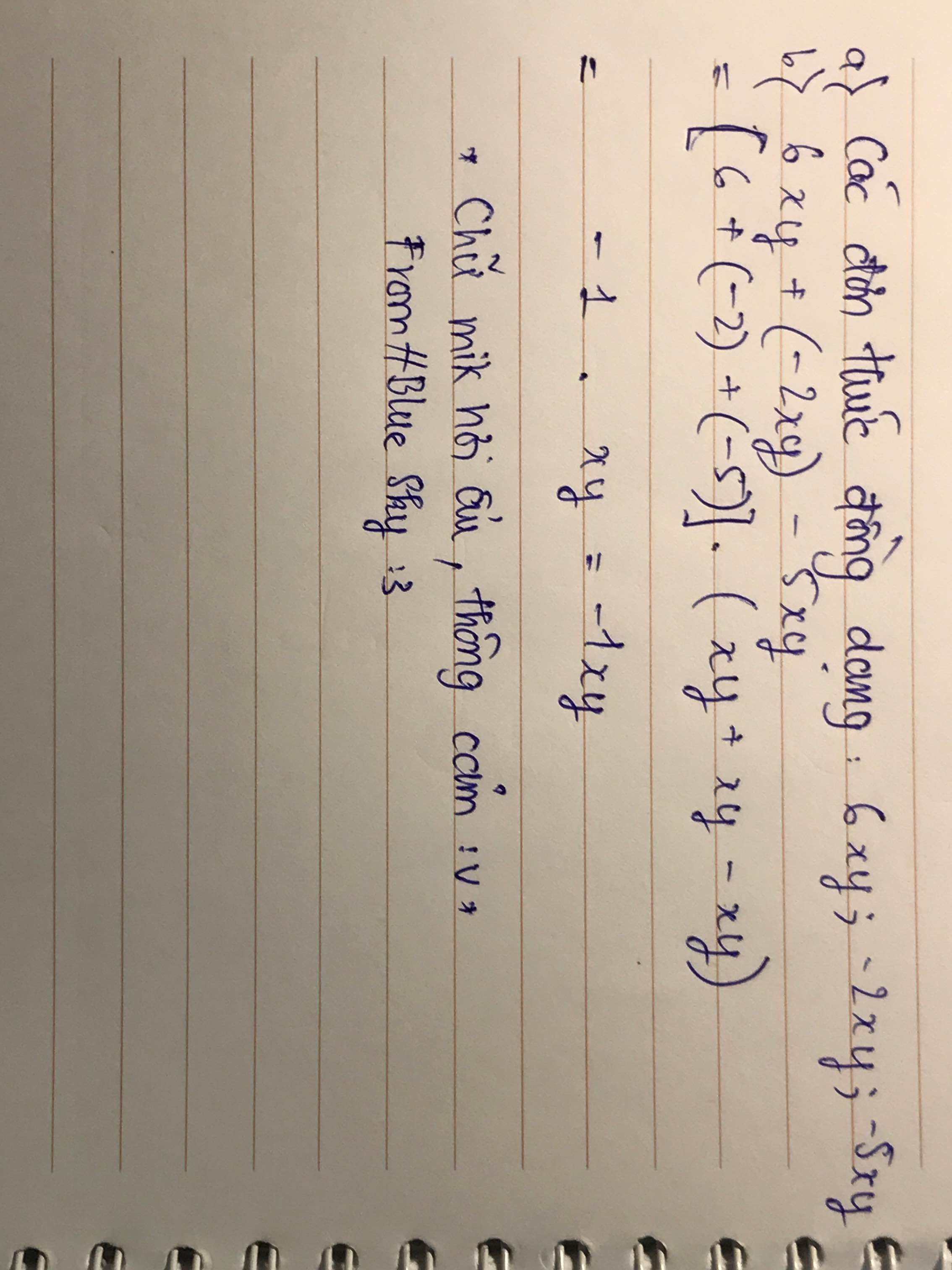cho các đơn thức sau. tìm và nhóm các đơn thức đồng dạng; 5x^2y^3; -5x^3y^2; 10x^3y^2;1/2x^2y^2;-3/4x^3y^2; -x^2y^2z

Những câu hỏi liên quan
thành các nhóm đơn thức đồng dạng trong các đơn thức sau,tính tổng xác đơn thức đồng dạng của mỗi nhóm -12x^2y,-3/8xyz,-100,-3yxz,-2xy.x,y.(-1/3xy)
Nhóm 1: -12x^2y;-2x^2y
=>Tổng là -14x^2y
Nhóm 2: -3/8xyz; -3xyz
=>Tổng là -27/8xyz
Nhóm 3: -1/3xy^2
Nhóm 4: -100
Đúng 0
Bình luận (0)
Có mấy nhóm đơn thức đồng dạng với nhau trong các đơn thức sau:
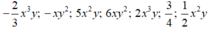
A. 2
B. 3
C. 4
D. 5
cho các đơn thức sau 5x mũ 2 y mũ 3; 10 mũ 3 y mũ 2; x mũ 2 y mũ 3; -3x mũ 3 y mũ 2;1/2 x mũ 2 y mũ 3 ; -5x mũ 3 y mũ 2; x mũ 2 y mũ 3 tìm và nhóm các đơn thức đồng dạng rồi tính tổng các đơn thức đó
Nhóm 1: 5x^2y^3;x^2y^3;1/2x^2y^3;x^2y^3
Tổng là 6,5x^2y^3
Nhóm 2: 10x^3y^2;-3x^3y^2;-5x^3y^2
Tổng là 2x^3y^2
Đúng 0
Bình luận (0)
Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng:
5
3
x
2
y
;
x
y
2
;
-
1
2
x
2
y
;
-
2
x
y
2
;
x
2
y
;...
Đọc tiếp
Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng: 5 3 x 2 y ; x y 2 ; - 1 2 x 2 y ; - 2 x y 2 ; x 2 y ; 1 4 x y 2 ; - 2 5 x 2 y ; x y
Các nhóm đơn thức đồng dạng là:
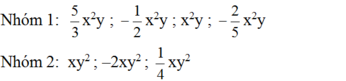
Vì nhóm 1 có phần biến chung là: x2y, nhóm 2 có phần biến chung là: xy2
Còn lại đơn thức xy (có phần biến là xy) không đồng dạng với các đơn thức nào đã cho.
Đúng 0
Bình luận (0)
xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng 5x2y; 3xy2; 2/3xy2;4/3x2yz;7x2y2;-2xy2;x2y;-1/5x2y2
bn có thể ghi theo công thức toán học đc ko
Đúng 0
Bình luận (0)
\(5x^2y;x^2y\)
\(3xy^2;\dfrac{2}{3}xy^2;-2xy^2\)
\(\dfrac{4}{3}x^2yz\)
\(7x^2y^2;-\dfrac{1}{5}x^2y^2\)
Đúng 2
Bình luận (0)
- 3xy^2, 2/3xy^2, -2xy^2.
- 5x^2
- 7x^2y^2, -1/5x^2y^2.
- 4/3x^2yz.
- x^2y
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Hãy xếp các đơn thức sau thành nhóm các đơn thức đồng dạng với nhau: -5x2yz; 3xy2z; 2/3 x2yz; 10x2y2z; - 2/3 xy2z; 5/7 x2y2z
Nhóm các đơn thức đồng dạng:
| -5x2yz; 2/3 x2yz | 3xy2z; -2/3 xy2z | 10x2y2z; 5/7 x2y2z |
Đúng 0
Bình luận (0)
Cho các đơn thức -3x²y; 7xy²; 6xy; 4x7; -2xy; -5xy A)Tìm các đơn thức đồng dạng. b)Tính tổng các đơn thức đồng dạng vừa tìm
a/ Tìm bậc của đơn thức -2x2y3
b/ Tìm các đơn thức đồng dạng trong các đơn thức sau:
5xy3 ; 5x2y3 ; -4x3y2 ; 11 x2y3
Cho các đơn thức sau:
-
x
y
2
,
2
x
2
y
2
,
-
1
3
x
y
2
,
3
x
y
2
v
à
3
4
x
2
y
Đơn thức đồng dạng với đơn thức
x
y
2...
Đọc tiếp
Cho các đơn thức sau: - x y 2 , 2 x 2 y 2 , - 1 3 x y 2 , 3 x y 2 v à 3 4 x 2 y
Đơn thức đồng dạng với đơn thức x y 2 là:
A. 0
B. 1
C. 2
D. 3
Các đơn thức đồng dạng là: -xy2, -1/3 xy2, 3xy2. Chọn D
Đúng 0
Bình luận (0)