xem hình và cho biết khẳng định nào chứng tỏ a//b A a b B 1 1 3 2 3 2 4
Đọc tiếp
xem hình và cho biết khẳng định nào chứng tỏ a//b
Những câu hỏi liên quan
Xem hình bên rồi cho biết trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
1
.
E
1
;
2
;
3
;
4
;
c
2
.
F
a
;
b
3
.
P...
Đọc tiếp
Xem hình bên rồi cho biết trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
1 . E = 1 ; 2 ; 3 ; 4 ; c 2 . F = a ; b 3 . P = 1 ; 2 ; 3 ; 4 ; 5 ; a ; b ; c
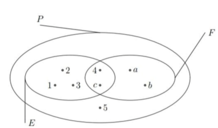
1. Đúng, vì tập hợp E có các phần tử 1;2;3;4;c
2. Sai, vì tập hợp F có các phần tử là a;b;c;4
3. Đúng, vì tập hợp P có các phần tử là các phần tử của tập hợp E; F và thêm phần tử 5
Đúng 0
Bình luận (0)
Bài 1: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a, Có các số tự nhiên a và b mà a thuộc Ư(b) và b thuộc Ư(a)
b, Nếu a là ước của b thì b : a cũng là ước của b.
Bài 2: Tìm các số tự nhiên n soa cho:
a, n + 1 là ước của 15
b, n + 5 là ước của 12
Bài 3: Chứng tỏ rằng 11 là ước của số có dạng abba.
Bài 1:
a, sai
b, đúng
Bài 2:
a, Ư(15) = {1;3;5;15}
Vì n + 1 là ước của 15 nên ta có:
n + 1 = 1 => n = 0
n + 1 = 3 => n = 2
n + 1 = 5 => n = 4
n + 1 = 15 => n = 14
Vậy...
b, Ư(12) = {1;2;3;4;6;12}
Vì n + 5 là ước của 12 nên ta có:
n + 5 = 1 => n = -4 (loại)
n + 5 = 2 => n = -3 (loại)
n + 5 = 3 => n = -2 (loại)
n + 5 = 4 => n = -1 (loại)
n + 5 = 6 => n = 1
n + 5 = 12 => n = 7
Vậy...
Bài 3:
Ta có: abba = 1000a + 100b + 10b + a
= (1000a + a) + (100b + 10b)
= (1000 + 1)a + (100 + 10)b
= 1001a + 110b
= 11.(91a + 10b)
Vì 11(91a + 10b) \(⋮\)11 nên 11 là ước của số có dạng abba
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Xem hình 8.55 rồi cho biết trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
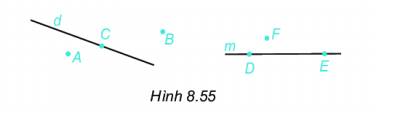
a) Điểm C thuộc đường thẳng d, hai điểm A và B không thuộc đường thẳng d.
b) Ba điểm A, B, C không thẳng hàng.
c) Điểm F không thuộc đường thẳng m
d) Ba điểm D, E, F không thẳng hàng.
a) Đúng vì điểm C nằm trên d và hai điểm A, B không nằm trên d.
b) Sai vì ta kẻ được đường thẳng đi qua cả 3 điểm A, B, C.
c) Đúng vì điểm F không nằm trên m.
d) Đúng vì F không nằm trên đường thẳng DE.
Đúng 1
Bình luận (0)
Cho tam giác ABC có A(1; -2; 3), B(0; 5; 6), C(1; 3; 2). Gọi H là hình chiếu vuông góc của A trên đường thẳng BC. Trong những khẳng định dưới đây, khẳng định nào sai? A. Một vectơ pháp tuyến của mặt phẳng (ABC) là: B. Một vectơ chỉ phương của đường thẳng AH là: C. AH ⊥ BC D. Các khẳng định trên không đồng thời đúng
Đọc tiếp
Cho tam giác ABC có A(1; -2; 3), B(0; 5; 6), C(1; 3; 2). Gọi H là hình chiếu vuông góc của A trên đường thẳng BC. Trong những khẳng định dưới đây, khẳng định nào sai?
A. Một vectơ pháp tuyến của mặt phẳng (ABC) là: 
B. Một vectơ chỉ phương của đường thẳng AH là: 
C. AH ⊥ BC
D. Các khẳng định trên không đồng thời đúng
Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
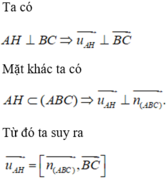
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.
Đúng 0
Bình luận (0)
Trong cuộc thi đấu bóng bàn có 6 đấu thủ A;B;C;D;E;F. Biết rằng có 2 đấu thủ vào chung kết và có các khẳng định sau:
1) A và B
2) B và E
3) A và F
4) B và F
5) C và A
Biết rằng có 4 khẳng định đúng một nửa và có 1 khẳng định sai hoàn toàn. Hãy cho biết 2 đấu thủ tham gia vong chung kết.
Lý luận sau đó ghi lời giải
Đố mấy người nà
Trong cuộc thi đấu bóng bàn có 6 đấu thủ A;B;C;D;E;F. Biết rằng có 2 đấu thủ vào chung kết và có các khẳng định sau:
1) A và B
2) B và E
3) A và F
4) B và F
5) C và A
Biết rằng có 4 khẳng định đúng một nửa và có 1 khẳng định sai hoàn toàn. Hãy cho biết 2 đấu thủ tham gia vong chung kết
Trong các khẳng định sau, khẳng định nào sai.
A. ƯC(5,20) {0; 1; 5}
B. ƯC(5,20) {1; 5}
C. ƯC(8,12) {1; 2; 4}
D. ƯC(6,9) {1; 3}
Câu 35: Tập hợp các ƯC(12,18,24) là.
A. {1; 2; 3}
B. {1; 2; 3; 6}
C. {1; 2; 3; 4}
D. {1; 2; 3; 4; 6}
Câu 36: ƯCLN(12,30) là.
A. 6
B. 5
C. 2
D. 10
Câu 37: ƯCLN(40, 60) là.
A. 40
B. 30
C. 20
D. 15
Câu 38: BCNN(3,4,6) là.
A. 72
B. 36
C. 12
D. 6
Giúp mình với nhé
Đọc tiếp
Trong các khẳng định sau, khẳng định nào sai. A. ƯC(5,20) = {0; 1; 5} B. ƯC(5,20) = {1; 5} C. ƯC(8,12) = {1; 2; 4} D. ƯC(6,9) = {1; 3} Câu 35: Tập hợp các ƯC(12,18,24) là. A. {1; 2; 3} B. {1; 2; 3; 6} C. {1; 2; 3; 4} D. {1; 2; 3; 4; 6} Câu 36: ƯCLN(12,30) là. A. 6 B. 5 C. 2 D. 10 Câu 37: ƯCLN(40, 60) là. A. 40 B. 30 C. 20 D. 15 Câu 38: BCNN(3,4,6) là. A. 72 B. 36 C. 12 D. 6 Giúp mình với nhé
Trong không gian Oxyz, cho đường thẳng d đi qua hai điểm A(2; 3; -1), B(1; 2; 4). Trong những khẳng định dưới đây, khẳng định nào sai? A.
AB
→
(-1; -1; 5) là một vectơ chỉ phương của đường thẳng d B. Phương trình chính tắc của đường thẳng d là: C. Đường thẳng d nằm trong hai mặt phẳng: (P): x - y + 1 0, (Q): 5x + z 0 D. Phương trình chính tắc của đường thẳng d là:
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d đi qua hai điểm A(2; 3; -1), B(1; 2; 4). Trong những khẳng định dưới đây, khẳng định nào sai?
A. AB → = (-1; -1; 5) là một vectơ chỉ phương của đường thẳng d
B. Phương trình chính tắc của đường thẳng d là: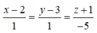 
C. Đường thẳng d nằm trong hai mặt phẳng: (P): x - y + 1 = 0, (Q): 5x + z = 0
D. Phương trình chính tắc của đường thẳng d là: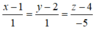 
Cho tam giác ABC với A(1; 4), B(3; -2), C(4; 5) và đường thẳng ∆: 2x – 5y + 3 = 0. Khẳng định nào sau đây là đúng?
A. Đường thẳng ∆ không cắt cạnh nào của tam giác
B. Đường thẳng ∆ cắt 1 cạnh của tam giác
C. Đường thẳng ∆ cắt 2 cạnh của tam giác
D. Đường thẳng ∆ cắt 3 cạnh của tam giác
A(1; 4), B(3; -2), C(4; 5)
Thay lần lượt tọa độ các đỉnh vào biểu thức P(x,y)= 2x – 5y + 3 ta có
P(1,4) = 2.1 – 5.4 + 3 = – 15, P(3, –2) = 2.3 – 5.( –2) + 3 = 19
P(4,5) = 2.4 – 5.5 + 3 = – 14
Do đó đường thẳng ∆ cắt các cạnh AB, BC và không cắt cạnh AC.
Đáp án C
Đúng 0
Bình luận (0)