Cho hình thang cân MNPQ,có 2 cạnh đáy MN và PQ ,chọn câu đúng
Những câu hỏi liên quan
cho hình thang cân MNPQ có độ dài cạnh đáy là MN = 7cm, độ dài cạnh đáy PQ gấp đôi độ dài cạnh đáy MN , độ dài chiều cao MH= 4cm.Tính diện tích hình thang cân ABCD?
PQ=7*2=14cm
\(S_{MNPQ}=\dfrac{1}{2}\cdot\left(7+14\right)\cdot4=2\cdot21=42\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho hình thang cân MNPQ (MN // PQ) có góc
M
Q
P
^
45
°
và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là: A. 728
c
m
2
. B. 346
c
m
2
. C. 364
c
m
2
. D. 362
c...
Đọc tiếp
Cho hình thang cân MNPQ (MN // PQ) có góc M Q P ^ = 45 ° và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:
A. 728 c m 2 .
B. 346 c m 2 .
C. 364 c m 2 .
D. 362 c m 2 .
Đáp án cần chọn là: C
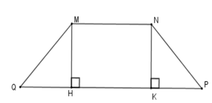
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 12 cm nên QH = KP = 40 − 12 2 = 14 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 12 + 40 ) .14 2 = 364 c m 2
Đúng 0
Bình luận (0)
Cho hình thang cân MNPQ (MN // PQ) có góc
M
Q
P
^
45
°
và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là: A. 418
c
m
2
. B. 209
c
m
2
C. 290
c
m
2
. D. 580...
Đọc tiếp
Cho hình thang cân MNPQ (MN // PQ) có góc M Q P ^ = 45 ° và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:
A. 418 c m 2 .
B. 209 c m 2
C. 290 c m 2 .
D. 580 c m 2 .
Đáp án cần chọn là: B
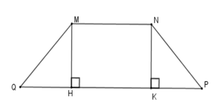
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 8 cm nên QH = KP = 30 − 8 2 = 8 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 8 + 30 ) .11 2 = 209 c m 2 .
Đúng 0
Bình luận (0)
cho hình thang cân MNPQ với cạnh đáy MN= 3cm, PQ và NP = 3cm, MP=7cm. tính độ dài MQ, NQ
SGK Toán 8 – Chân trời sáng tạo
21 tháng 7 2023 lúc 22:18
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân \(MNPQ\) (Hình 13) với hai đáy \(MN = 6cm\), \(PQ = 10\)cm và độ dài hai đường chéo \(MN = NQ = 8\sqrt 2 \) cm. Tính độ dài đường chéo và cạnh bên của hình thang
SGK Toán 8 – Chân trời sáng tạo
21 tháng 7 2023 lúc 22:14
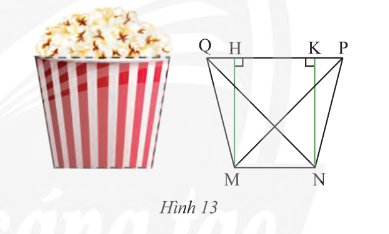
Tìm các đoạn thẳng bằng nhau trong hình thang cân \(MNPQ\) có hai đáy \(MN\) và \(PQ\)
MNPQ là hình thang cân
=>MP=NQ và MQ=NP
Đúng 0
Bình luận (0)
cho hình thang cân MNPQ có đáy nhỏ MN và hai đường chéo cắt nhau tại B và hai cạnh bên cắt nhau tại A
a) chứng minh tam giác AMN cân
b) chứng minh AB là trung trực của MN và PQ
a) Ta có: góc Q =góc P
=> AQ = AP ( quan hệ giữa góc và cạnh đối diện)
Ta có: AM + MQ = AQ
AN + NP = AP
Mà MQ = NP ( MNPQ là hình thang cân).
AQ = AP (cmt)
=> AM = AN => tam giác MAN cân tại A.
Câu b bạn tự làm nha
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN//BS, NP//CD, MQ // CD. Những khẳng định nào sau đây là đúng?1) PQ // SA(2) PQ // MN(3) tứ giác MNPQ là hình thang(4) tứ giác MNPQ là hình bình hành A. (4) B. (1) và (3) C. (2) và (3) D. (2) và (4)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN//BS, NP//CD, MQ // CD. Những khẳng định nào sau đây là đúng?
1) PQ // SA
(2) PQ // MN
(3) tứ giác MNPQ là hình thang
(4) tứ giác MNPQ là hình bình hành
A. (4)
B. (1) và (3)
C. (2) và (3)
D. (2) và (4)
Đáp án B
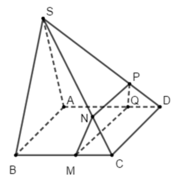
Ta có: MN // BS ⇒ C M C B = C N C S
MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A
NP // CD ⇒ C N C S = D P D S
Do đó: D P D S = D Q D A PQ // SA (Định lý Ta - lét trong tam giác SAD)
Lại có MN // BS và SB ∩ SA = S
Do đó MN không thể song song với PQ
Xét tứ giác MNPQ có NP // MQ (//CD)
Do đó MNPQ là hình thang.
Vậy khẳng địn (1) và (3) đúng.
Đáp án B
Đúng 0
Bình luận (0)
Đây là câu hỏi nâng cao : Cho hình thang cân MNPQ (MN//PQ). Chứng MN +PQ
