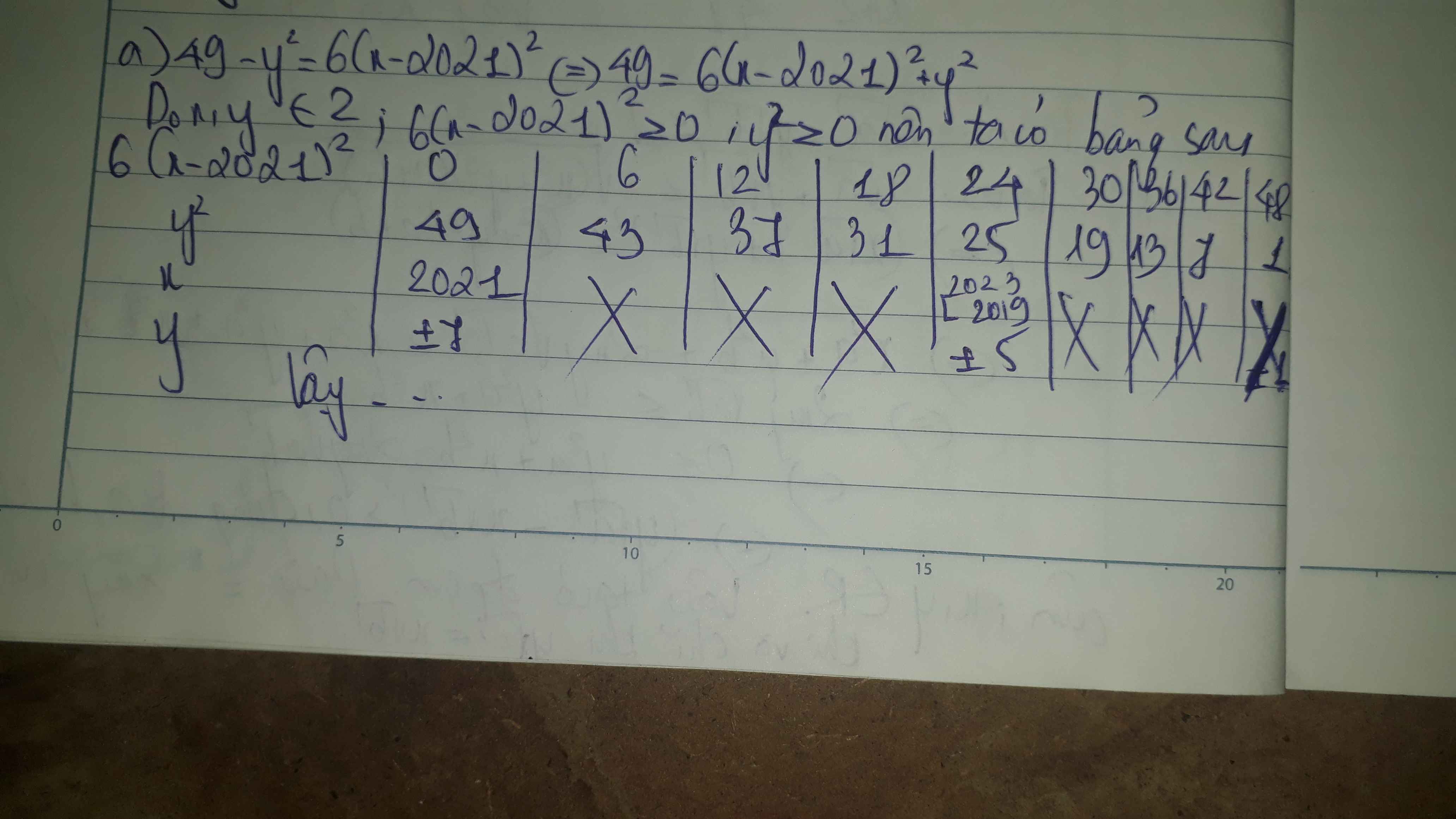tìm x,y nguyên biết xy^2-2xy+5y=15.giúp mình nha...

Những câu hỏi liên quan
Tìm số nguyên x biết
a,3x+3y-2xy=7
b,xy+2x+y+11=0
c,xy+x-y=4
d,2x.(3y-2)+(3y-2)=12
e,3x+4y-xy=15
f,xy+3x-2y=11
g,xy+12=x+y
h,xy-2x-y=-6
i,xy+4x=25+5y
ii,2xy-6y+x=9
iii,xy-x+2y=3
k,2.x^2.y-x^2-2y-2=0
l,x^2.y-x+xy=6
Tìm x, y nguyên thỏa mãn:
a) x - 2xy + y = 0
b) 2xy + x- 2y = 4
c) 3xy - 2x +5y = 29
d) 25 - y^2 = 8 . ( x - 2009 )^2
e) 6x^2 + 5y^2 = 74
f) y^2 + 8 . ( x - 2010 )^2 = 36
Giúp mình nha mai cô kiểm tra rồi, ai làm được phần nào thì làm xong mình sẽ tick cho nhé
#Toán_7
Lần trước phần a) mình đăng nhầm nhé xin lỗi nha giúp mình với ạ-------NYA-------
\(6x^2+5y^2=74\Rightarrow5y^2\le74\Rightarrow y^2< 16\Rightarrow\left|y\right|< 4\Rightarrow-4< y< 4\)(1)
e,\(5y^2⋮2\Rightarrow y^2⋮2\Rightarrow y⋮2\)(2)
Từ (1) và (2) kết hợp với y là số nguyên thì \(y\in\left\{-2;0;2\right\}\)
Thay vào đề bài thử loại y = 0 ta được 4 cặp số thỏa mãn là:
\(\left(x;y\right)\in\left\{\left(3;2\right),\left(3;-2\right),\left(-3;2\right),\left(-3;-2\right)\right\}\)
Đúng 0
Bình luận (0)
a)\(x-2xy+y=0\)
\(\Leftrightarrow2x-4xy+2y=0\)
\(\Leftrightarrow2x\left(1-2y\right)-\left(1-2y\right)=-1\)
\(\Leftrightarrow\left(2x-1\right)\left(1-2y\right)=-1\)
\(\Leftrightarrow\left(2x-1\right)\left(2y-1\right)=1=1.1=-1.-1\)
giải ra ta đc (x;y)= (0;0) ; (1;1)
Đúng 0
Bình luận (0)
tìm các cặp số nguyên x,y biết (x-1)(xy-2)=5 trả lời giúp mình nha chiều kt 15 phút
Bài 1:
Tìm x € Z biết |6x-3|=15
Bài 2:
Tìm cặp (x,y) nguyên , biết
x+xy+y=9
Giúp mình nha!!!
1) |6x-3|=15
=> 6x-3 = 15 hoặc 6x-3 = -15
=> x=3 hoặc x=-2
2) x+xy+y=9
<=> x(y+1) +y=9
<=> x(y+1) +(y+1) = 10
<=> (x+1)(y+1)=10= -2.-5 =-5.-2 = -1.-10 = -10.1 = 2.5=5.2=1.10=10.1
Từ đây có thể tìm đc x và y nhé!
CHÚC BẠN HỌC TỐT!
Đúng 0
Bình luận (0)
Bài 1:
\(\left|6x-3\right|=15\Rightarrow\orbr{\begin{cases}6x-3=-15\\6x-3=15\end{cases}\Rightarrow}\orbr{\begin{cases}6x=-12\\6x=18\end{cases}\Rightarrow}\orbr{\begin{cases}x=-2\\x=3\end{cases}}\)
Bài 2:
\(x+xy+y=9\Leftrightarrow x+xy+y+1=10\Leftrightarrow x\left(1+y\right)+\left(y+1\right)=10\)
\(\Leftrightarrow\left(x+1\right)\left(y+1\right)=10\)
Ta có bảng sau:
| x+1 | -10 | -5 | -2 | -1 | 1 | 2 | 5 | 10 |
| y+1 | -1 | -2 | -5 | -10 | 10 | 5 | 2 | 1 |
| x | -11 | -6 | -3 | -2 | 0 | 1 | 4 | 9 |
| y | -2 | -3 | -6 | -11 | 9 | 4 | 1 | 0 |
Vậy có 8 cặp số nguyên thỏa mãn là ........
Đúng 0
Bình luận (0)
Tìm x, y nguyên thỏa mãn:
a) x - 2xy + x = 0
b) 2xy + x- 2y = 4
c) 3xy - 2x +5y = 29
d) 25 - y^2 = 8 . ( x - 2009 )^2
e) 6x^2 + 5y^2 = 74
f) y^2 + 8 . ( x - 2010 )^2 = 36
Giúp mình nha mai cô kiểm tra rồi, ai làm được phần nào thì làm xong mình sẽ tick cho nhé
#Toán_7
a) \(x-2xy+x=0\Leftrightarrow2x-2xy=0\)
\(\Leftrightarrow2x\left(1-y\right)=0\Leftrightarrow\hept{\begin{cases}2x=0\\1-y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=1\end{cases}}\)
Đúng 0
Bình luận (0)
b) \(2xy+x-2y=4\)
\(\Leftrightarrow x\left(2y+1\right)-2y-1=3\)
\(\Leftrightarrow x\left(2y+1\right)-\left(2y+1\right)=3\)
\(\Leftrightarrow\left(2y+1\right)\left(x-1\right)=3\)
Đến đây bí =) Alibaba!
Đúng 0
Bình luận (0)
\(a)x-2xy+x=0\)
\(\Leftrightarrow2x-2xy=0\)
\(\Leftrightarrow2x\left(1-y\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x=0\\1-y=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\y=1\end{cases}}}\)
Vậy \(x=0;y=1\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
B1 . Tìm các số nguyên x,y biết \(x^2-2x+2xy=3+4y\)
B2. Tìm x,y,z biết : \(|2x-3y|+|5y-7z|+|x^2-y^2-2.z^2-45|=0\)
Giúp mình với mai mình phải nộp rồi
XONG RỒI ĐẤY BẠN
a) \(x^2-2x+2xy=3+4y\)
\(x^2-2x+2xy-4y=3\)
\(x\left(x-2\right)+2y\left(x-2\right)=3\)
\(\left(x-2\right)\left(x+2y\right)=3\)
\(\Rightarrow x-2;x+2y\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\)Ta có bảng giá trị:
| \(x-2\) | \(1\) | \(-1\) | \(3\) | \(-3\) |
| \(x+2y\) | \(3\) | \(-3\) | \(1\) | \(-1\) |
| \(x\) | \(3\) | \(1\) | \(5\) | \(-1\) |
| \(y\) | \(0\) | \(-2\) | \(-2\) | \(0\) |
Vậy, \(\left(x;y\right)\in\left\{\left(3;0\right);\left(1;-2\right);\left(5;-2\right)\left(-1;0\right)\right\}\)
b) \(\left|2x-3y\right|+\left|5y-7z\right|+\left|x^2-y^2-2z^2-45\right|=0\)
Ta có: \(\left|2x-3y\right|\ge0\)
\(\left|5y-7z\right|\ge0\)
\(\left|x^2-y^2-2z^2-45\right|\ge0\)
\(\Rightarrow\left|2x-3y\right|+\left|5y-7z\right|+\left|x^2-y^2-2z^2-45\right|\ge0\)
Mà đề cho \(\left|2x-3y\right|+\left|5y-7z\right|+\left|x^2-y^2-2z^2-45\right|=0\)
\(\Rightarrow\hept{\begin{cases}\left|2x-3y\right|=0\\\left|5y-7z\right|=0\\\left|x^2-y^2-2z^2-45\right|=0\end{cases}\Rightarrow\hept{\begin{cases}2x-3y=0\\5y-7z=0\\x^2-y^2-2z^2-45=0\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}2x=3y\\5y=7z\\x^2-y^2-2z^2=45\end{cases}\Rightarrow\hept{\begin{cases}10x=15y\\15y=21z\\x^2-y^2-2z^2=45\end{cases}}}\)
\(\Rightarrow10x=15y=21z\Rightarrow\frac{x}{21}=\frac{y}{14}=\frac{z}{10}\Rightarrow\frac{x^2}{21^2}=\frac{y^2}{14^2}=\frac{z^2}{10^2}\)và \(x^2-y^2-2z^2=45\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\frac{x^2}{21^2}=\frac{y^2}{14^2}=\frac{z^2}{10^2}=\frac{2z^2}{2\cdot10^2}=\frac{x^2-y^2-2z^2}{21^2-14^2-2\cdot10^2}\)
\(=\frac{45}{441-196-200}=1\)(vì \(x^2-y^2-2z^2=45\))
\(\Rightarrow\hept{\begin{cases}x^2=21^2\\y^2=14^2\\z^2=10^2\end{cases}}\Rightarrow\hept{\begin{cases}x=21\\y=14\\z=10\end{cases}}\)
Vậy, \(\left(x;y;z\right)=\left(21;14;10\right)\)
Đúng 0
Bình luận (0)
Tìm x, y nguyên thỏa mãn:
a) x - 2xy + x = 0
b) 2xy + x- 2y = 4
c) 3xy - 2x +5y = 29
d) 25 - y^2 = 8 . ( x - 2009 )^2
e) 6x^2 + 5y^2 = 74
f) y^2 + 8 . ( x - 2010 )^2 = 36
Giúp mình nha mai cô kiểm tra rồi, ai làm được phần nào thì làm xong mình sẽ tick cho nhé
#Toán_7
Lần trước đăng nhầm nhé heheee
a,\(x-2xy+x=0=>2x-2xy=0=>2x\left(1-y\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\1-y=0\end{cases}\Rightarrow\orbr{\begin{cases}0\\1\end{cases}}}\)
Đúng 0
Bình luận (0)
bài 1 ; tìm x bt
a,3.(x+3)-2.(x-5)=11
b,14-4./x/=-6
bài 2 tìm x,y nguyên biết
a,(x-2).(6+y)=(-19)
b,2xy - 3x +20= 0
c, xy+2y+3x+15=0
giúp mk nha, mk cần gấp
a, 3(x+3)-2(x-5)=11
=> 3x+9-2x+10=11
=> 3x-2x=11-10-9
=> x=-8
Vậy.........
b, 14-4|x|=-6
=> -4|x|=8
=> |x|=-2(VL vì trị tuyệt đối luôn lớn hơn hoặc = 0)
Vậy......
Giúp mình vs
Tìm x,y thuộc Z
a)49-y^2=6(x-2021)^2
b)x^2 + xy + y^2=2x+y
c)x^2 + xy + y^2=x+y
d)x^2 + 3xy + 3y^2 =3y
e)x^2 - 2xy - 5y^2=y+1
Bài b:
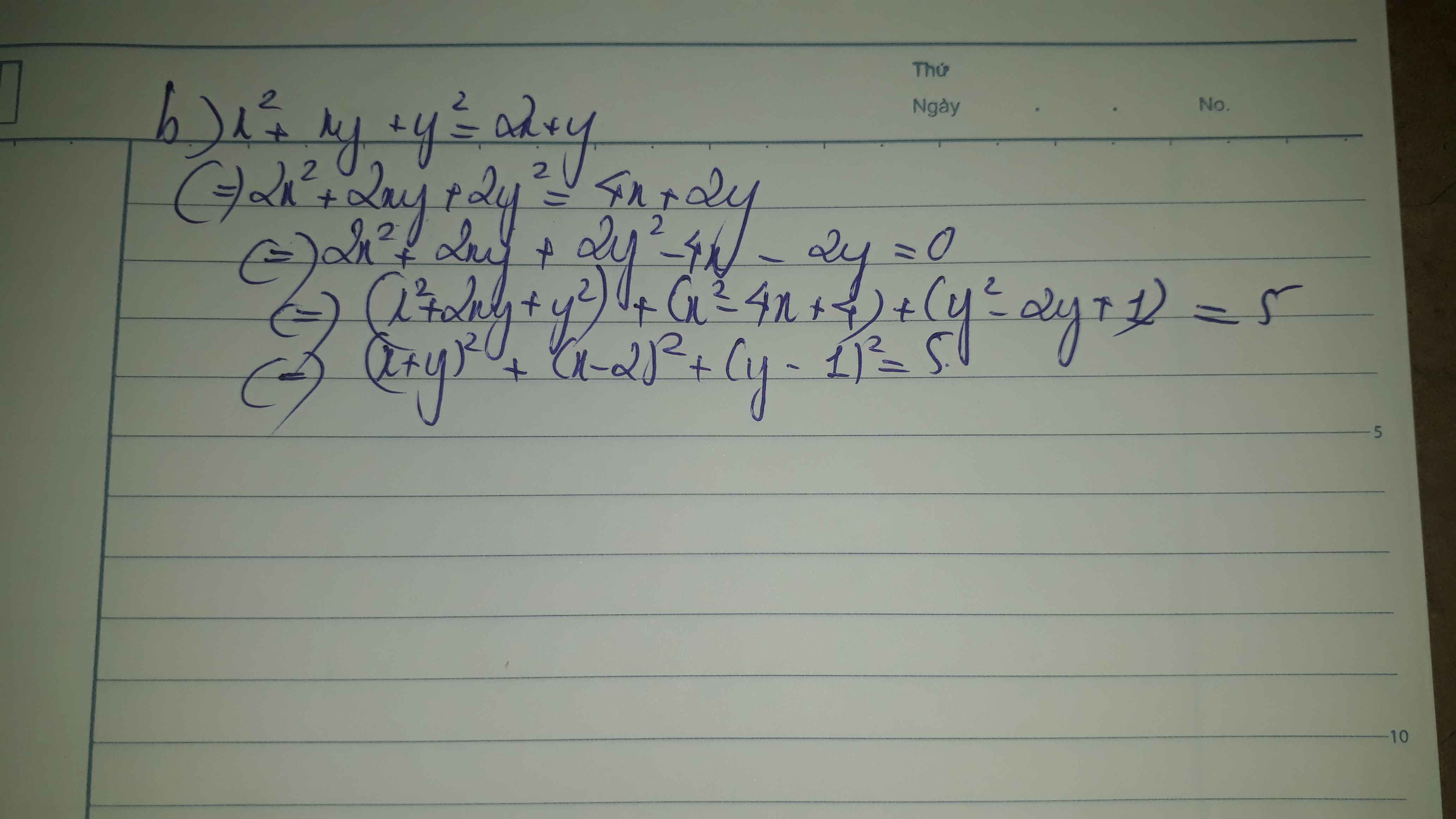
Đến đoạn này bạn xét như bài a nhé.
Bài c cũng tương tự câu b, bạn nhân 2 vào cả 2 vế, chuyển vế đổi dấu và ghép vế trái lại thành tổng các bình phương, vế phải là một số tự nhiên. Đến đoạn này cũng xét như bài a.
Còn bài d và bài e thì mình chưa biết làm thế nào, nhưng mình nghĩ vế trái sẽ là bình phương của tổng hoặc hiệu của x và y, vế phải là bình phương của tổng hoặc hiệu của y và một số nào đó. Tuy nhiên chắc là sẽ phải nhân thêm một số nào đó bởi vì nếu không nhân khi làm sẽ ra phân số, không xét được.
Đúng 1
Bình luận (0)