Tìm a,b thuộc Z để đa thức A(x)=x2+ax+b chẵn với mọi x thuộc R.

Những câu hỏi liên quan
Các số nguyên p,q phải thoả mãn điều kiện gì để:
a) Đa thức P(x)=x^2+px+q có giá trị là số chẵn với mọi x thuộc Z
b) Đa thức Q(x)=x^3+px+q có giá trị là bội của 3 với mọi x thuộc Z
a, để p(x) là số chẵn với mọi x thuộc z thì:
p(0)=q là số chẵn
p(1)=1^2+p*1+q là số chẵn
Mà q là số chẵn nên 1+p là số chẵn
suy ra p là số lẻ
suy ra nếu q là số chẵn, p là số lẻ thì p(x)là số chẵn với mọi x thuộc z
Đúng 0
Bình luận (0)
Cho đa thức
f(x)=ax+b ; g(x)=cx+d
a) CMR: Nếu f(x) = g(x) với mọi x thuộc R thì a=c và b=d
b) Gỉa sử f(x) khác g(x) với mọi x thuộc R
Tìm điều kiện a,b,c,d để f(x) và g(x) ko nhận giá trị nào bằng nhau
Cho đa thức
f(x)=ax+b
Tìm điều kiện của a và b để f(x1+x2)=f(x1)+f(x2) với mọi x thuộc R
ngu không biết làm bài này, mày đúng là ngu hết nói nổi
Đúng 0
Bình luận (0)
Cho thức B= x2-x+2/x-3 với x ≠ 3
a) Tìm x để B<0
b) Tìm x thuộc Z để B thuộc Z:
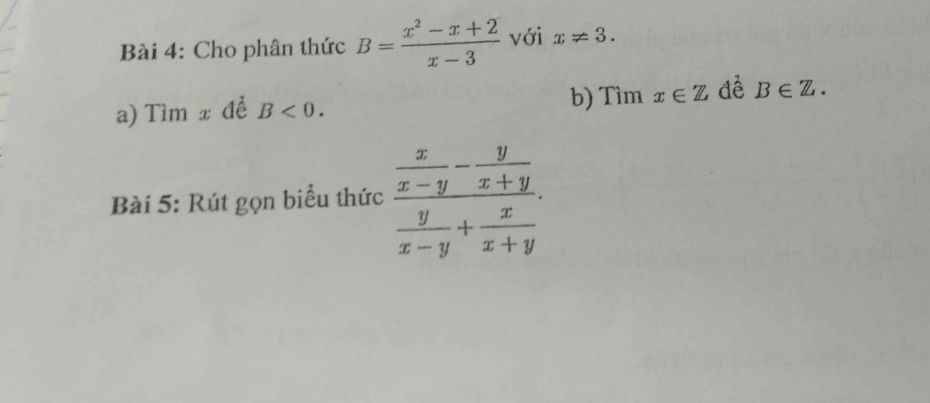
Bài 4:
a. Ta thấy: $x^2-x+2=(x-\frac{1}{2})^2+1,75>0$ với mọi $x$.
Do đó để $B=\frac{x^2-x+2}{x-3}<0$ thì $x-3<0$
$\Leftrightarrow x<3$
b.
$B=\frac{x(x-3)+2(x-3)+8}{x-3}=x+2+\frac{8}{x-3}$
Với $x$ nguyên, để $B$ nguyên thì $x-3$ phải là ước của 8.
$\Rightarrow x-3\in\left\{\pm 1; \pm 2; \pm 4; \pm 8\right\}$
$\Rightarrow x\in \left\{4; 2; 5; 1; -1; 7; 11; -5\right\}$
Đúng 1
Bình luận (0)
Bài 5:
\(\frac{\frac{x}{x-y}-\frac{y}{x+y}}{\frac{y}{x-y}+\frac{x}{x+y}}=\frac{\frac{x(x+y)-y(x-y)}{(x-y)(x+y)}}{\frac{y(x+y)+x(x-y)}{(x-y)(x+y)}}\)
\(=\frac{x(x+y)-y(x-y)}{y(x+y)+x(x-y)}=\frac{x^2+y^2}{x^2+y^2}=1\)
Đúng 0
Bình luận (0)
Cho đa thức f(x) = ax + b
Tìm điều kiện của các hằng số a,b để:
f(x1 + x2) = f(x1) + f(x2) [Với mọi x thuộc R]
\(f\left(x1\right)=ax1+b;f\left(x2\right)=ax2+b;f\left(x1+x2\right)=a\left(x1+x2\right)+b\)
f(x1+x2)=ax1+ax2+b=ax1+ax2+2b
=> b=0; mọi a
Đúng 0
Bình luận (0)
cho đa thức f(x)=ax mũ 3 + bx mũ 2 + cx + d (a,b,c,d thuộc z) biết f(x) chia hết cho 5 với mọi x thuộc z . Chứng minh rang : a,b,c,d chia hết cho 5
Ta có: x là số nguyên và x chia hết cho 5
=> \(ax^3\)chia hết cho 5
\(bx^2\)chia hết cho 5
\(cx\)chia hết cho 5
\(d\)chia hết cho 5
Suy ra cả a,b,c,d đều chia hết cho 5
Đúng 0
Bình luận (0)
cho đa thức f(x)=ax mũ 3 + bx mũ 2 + cx + d (a,b,c,d thuộc z) biết f(x) chia hết cho 5 với mọi x thuộc z . Chứng minh rang : a,b,c,d chia hết cho 5
Cho đa thức: \(P\left(x\right)=ax^2+bx+c\). Biết P(x)>0 với mọi x thuộc R và a>0. CM: \(\dfrac{5a-3b+2c}{a-b+c}>1\)
Cho đa thức: \(P\left(x\right)=ax^2+bx+c\). Biết P(x)>0 với mọi x thuộc R và a>0.CM: \(\dfrac{5a-3b+2c}{a-b+c}>1\)











