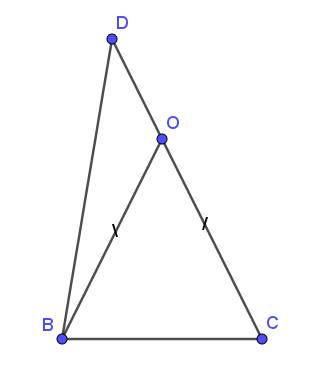
Cho tam giác OBC cân ở O . Trên tia đối của tia OC lấy điểm A . Chứng minh AB<AC

Những câu hỏi liên quan
Bài 1: Cho▲ABC cân tại A; Trên tia đối của BCC lấy điểm D; trên tia đối CB lấy điểm E sao cho BDCEa. Chứng minh ▲ADE cânb. Kẻ BH⊥AD (H∈AD) kẻ CK⊥AE (K∈AE). Chứng minh BHCKc. Gọi O là giao điểm của BH và CK. Tam giác OBC là tam giác y.Bài 2: Cho ▲ABC vuông cân tại A; Trên cạnh AB lấy điểm D; trên cạnh AC lấy điểm E sao cho AD:AE. Các đường thẳng vuông góc kẻ từ A; E với CD cắt BC ở G và H. Đường thẳng EH cắt AB ở M. Đường thẳng kẻ từ A và //BC cắt MH ở Ia. ▲ACD▲AMEb. ▲AGB▲MIAc. BGGH.*Mọi người gi...
Đọc tiếp
Bài 1: Cho▲ABC cân tại A; Trên tia đối của BCC lấy điểm D; trên tia đối CB lấy điểm E sao cho BD=CE
a. Chứng minh ▲ADE cân
b. Kẻ BH⊥AD (H∈AD) kẻ CK⊥AE (K∈AE). Chứng minh BH=CK
c. Gọi O là giao điểm của BH và CK. Tam giác OBC là tam giác y.
Bài 2: Cho ▲ABC vuông cân tại A; Trên cạnh AB lấy điểm D; trên cạnh AC lấy điểm E sao cho AD:AE. Các đường thẳng vuông góc kẻ từ A; E với CD cắt BC ở G và H. Đường thẳng EH cắt AB ở M. Đường thẳng kẻ từ A và //BC cắt MH ở I
a. ▲ACD=▲AME
b. ▲AGB=▲MIA
c. BG=GH.
*Mọi người giúp mik giải bài tập nha. Cảm ơn mn nhiều ạ*
1:
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
b: Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
góc HDB=góc KEC
=>ΔHBD=ΔKCE
=>HB=KC
c: góc HBD=góc KCE
=>góc OBC=góc OCB
=>ΔOBC cân tại O
Đúng 1
Bình luận (1)
Cho tam giác OBC có OB = OC
Trên tia đối của tia OC lấy điểm D. Chứng minh DB<DC
Xem chi tiết
Trên tia đối của tia OC lấy điểm D. Chứng minh DB<DC
Lời giải:
Xét tam giác $OBD$, áp dụng BĐT tam giác thì:
$DB< OB+OD$
Mà $OB=OC$ nên: $OB+OD=OC+OD=CD$
$\Rightarrow DB< CD$ (đpcm)
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE.
a) chứng minh rằng : tam giác ABD = tam giác ACE
b) kẻ BI vuông góc AD, CK vuông góc AE, chúng cắt nhau tại O. Chứng minh rằng tam giác OBC cân.
c) nếu tam giác ABC đều và DB = CE = BC thì tam giác OBC là tam giác gì?
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM CN.a) Chứng minh: ΔAMN là tam giác cân.b) Kẻ BH ⊥ AM (H ∈ AM),kẻ CK ⊥ AN (K ∈ AN). Chứng minh: BH CKc) Chứng minh : AH AKd) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?e) Khi ∠BAC 600và BM CN BC, hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC.
Đọc tiếp
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN.
a) Chứng minh: ΔAMN là tam giác cân.
b) Kẻ BH ⊥ AM (H ∈ AM),kẻ CK ⊥ AN (K ∈ AN). Chứng minh: BH = CK
c) Chứng minh : AH = AK
d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?
e) Khi ∠BAC = 600và BM = CN =BC, hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC.
Tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD CE. Kẻ BH vuông góc với AD. Kẻ CK vuông góc với AE. c) Gọi O là giao điểm của HB và KC. Chứng minh: OBC cân. d) Chứng minh: AO là tia phân giác của góc DAE e) Gọi I là trung điểm của BC. Chứng minh: A, I, O thẳng hàng.
Đọc tiếp
Tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông góc với AD. Kẻ CK vuông góc với AE.
c) Gọi O là giao điểm của HB và KC. Chứng minh: OBC cân.
d) Chứng minh: AO là tia phân giác của góc DAE
e) Gọi I là trung điểm của BC. Chứng minh: A, I, O thẳng hàng.
c: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó:ΔABD=ΔACE
Suy ra: \(\widehat{HDB}=\widehat{KEC}\)
Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HDB}=\widehat{KEC}\)
Do đó: ΔHBD=ΔKCE
Suy ra: \(\widehat{HBD}=\widehat{KCE}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
d: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO⊥BC
=>AO⊥DE
Ta có: ΔADE cân tại A
mà AO là đường cao
nên AO là tia phân giác của góc DAE
e: Ta có: IB=IC
nên I nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,I,O thẳng hàng
Đúng 5
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M , trên tia đối của tia CB lấy điểm N sao cho BM=BC=CN.Kẻ BH vuông góc với AM,CK vuông góc với AN , gọi O là giao điểm của 2 đường thẳng HB và KC
a)Chứng minh AM=AN
b)Chứng minh hai tam giác BHM=CKN
C)Chứng minh tam giác OBC cân
a) ABC cân tại A (gt) => AB=AC và góc ABC = góc ACB
=> góc ABM = góc ACN ( các góc kề bù với góc ABC và góc ACB)
Xét tam giác ABM và tam giác ACN có
AB=AC
góc ABM= góc ACN (cmt)
BM=CN )gt)
=> tam giác ABM = tam giác ACN ( c.g.c)
=> AM=AN ( 2 cạnh tương ứng)
b) tam giác ABM = tam giác ACN (cmt)
=> góc M= góc N (cặp góc tương ứng)
Xét tam giác HBM và tam giác KCN có
góc BHM= góc CKN =90 độ (BH vuông góc AM, AN vuông góc CK)
BM = CN (Gt)
góc M= góc N (cmt)
=> tam giác HBM = tam giác KCN ( cạnh huyền - góc nhọn)
c) TA có tam giác HBC và tam giác KCN (cmt)
=> góc HBM = góc KCN (hai goc tương ứng)
MÀ góc HBM = góc CBO ( hai góc đối đỉnh )
góc KCN=góc BCO ( hai góc đối đỉnh )
=> góc CBO= góc BCO
=> tam giác OBC cân tại O ( dấu hiệu nhận biết tam giác vuông)
câu c nhầm là dấu hiệu nhận biết tg cân ms đúng

a) \(\Delta\)ABC cân tại A => ^ABC = ^ACB => ^ABM = ^ACN
Xét \(\Delta\)ABM và \(\Delta\)ACN có: AB = AC; ^ABM = ^ACN; BM = CN
=> \(\Delta\)ABM = \(\Delta\)ACN
=> AM = AN
b) (a) => \(\Delta\)AMN cân tại A => ^AMN = ^ANM => ^HMB = ^KNC
Xét \(\Delta\)HMB và \(\Delta\)KNC có: MB = CN; ^HMB = ^KNC ; ^MHB = ^NKC = 90o
=> \(\Delta\)HMB = \(\Delta\)KNC
=> ^HBM = ^KCN
=> ^OBC = ^OCB
=> \(\Delta\)OBC cân.
Xem thêm câu trả lời
tam giác ABC cân tại a.trên tia đối của tia BC lấy D ,trên tia đối của tia CB lấy E sao cho BD=CE .
a,chứng minh tam giác ADE cân .
b,kẻ BH vuông góc với AB ,CK vuông góc với AE. chứng minh BH=CK, HK=BC
c,O là giao của HB và KC ,tam giác OBC là tam giác gì ?vì sao ?
d, M là TĐ BC chứng minh AM, BH, CK đồng quy
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=AD.
a) Gọi O là giao điểm của BH và CK. Tam giác OBC là tam giác gì? Vì sao?.
b) Gọi M là trung điểm BC chứng minh rằng AM, BH, CK đồng quy
Bài 3: Cho tam giác OBC vuông tại O, M là trung điểm của BC. Trên tia đối của tia MO lấy điểm D sao cho MO = MD
. a) Chứng minh OB = DC, OB // CD
b) Gọi E là trung điểm của OC. Trên tia đối của tia EM lấy điểm K sao cho ME=EK. Chứng minh OK // MC; KC // MD
c) Chứng minh ME ⊥OC.
a) xét tứ giác BDCO có:
M là trung điểm BC (gt)
D là điểm đối xứng của O qua M (D thuộc tia đối MO; MO=MD)
=> tứ giác BDCO là hình bình hành (vì có 2 đường chéo cắt nhau tại giao điểm)
=> OB=DC và OB//CD (tính chất hình bình hành)
b) xét tam giác COM có: OM=MC (do OD và BC cắt nhau tại giao điểm)
=> tam giác COM là tam giác cân tại M
xét tam giác cân COM cân tại M có E là trung điểm của OC
=> ME là đường trung tuyến của tam giác cân COM
mà trong tam giác cân đường trung tuyến trùng với đường cao
=> ME là đường cao của tam giác COM => ME _|_ OC
Mà E là trung điểm OC => ME là đường trung trực của đường thẳng OC
xét tứ giác OMCK có: ME là đường trung trực của OC
=> tứ giác OMCK là hình thoi
=> CK//OM và OK//MC (tính chất hình thoi)
c) Ở trên câu b) chứng minh rồi