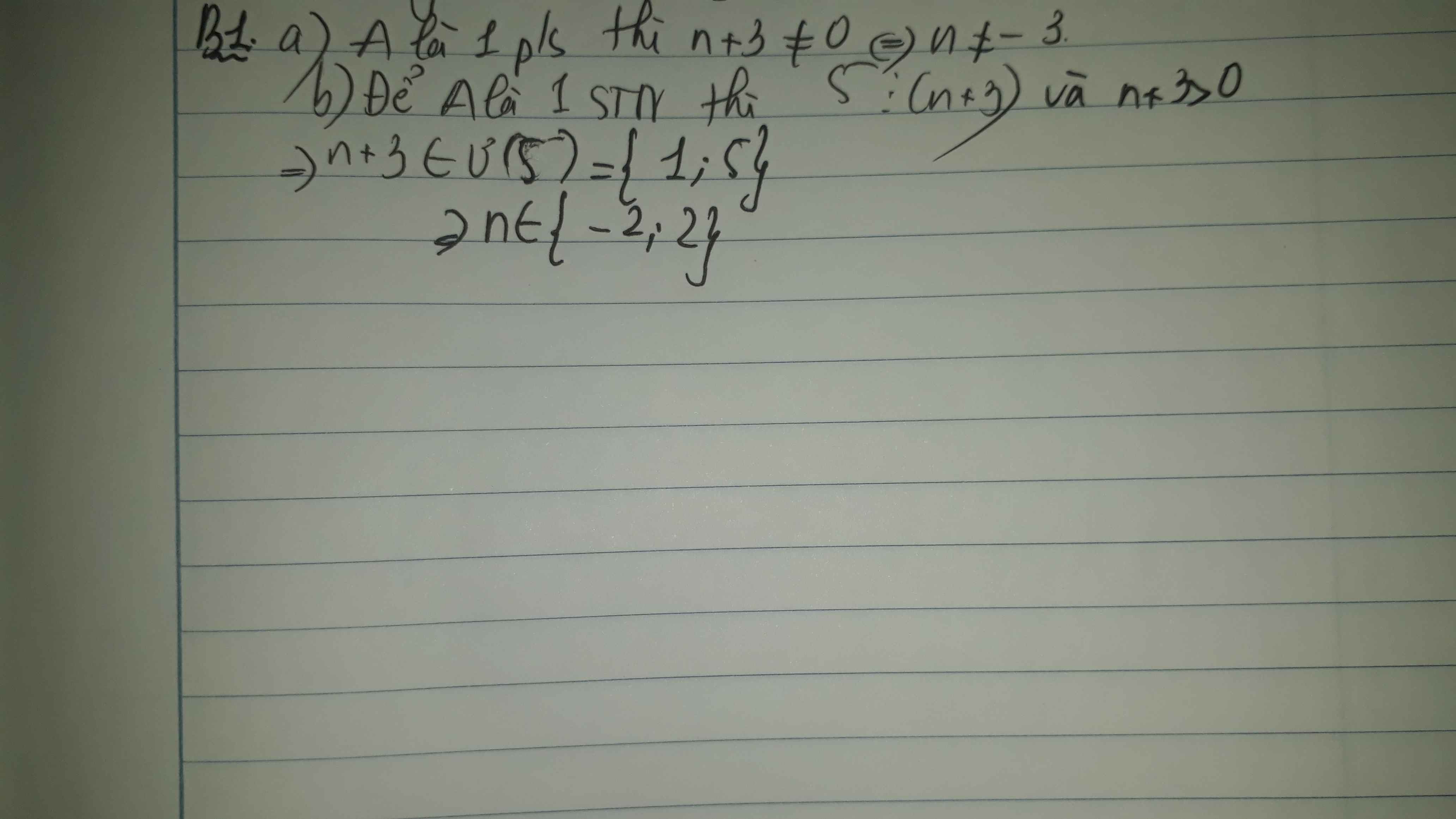Bài 1:

Ta có: (3a+1)(b-5)=21=1.21=21.1=3.7=7.3. Kẻ bảng:

+/ 3a+1=1=>a=0

    b-5=21=>b=26

+/ 3a+1=21 => a=20/3 (Loại)

+/ 3a+1=3 => a=2/3 (Loại)

+/ 3a+1=7 => a=2

    b-5=3 => b=8

ĐS: a,b ={(0, 26); (2, 8)}

Bài 2:

Ta có: 3n+4 chia hết cho 2n-1 => 2(3n+4) chia hết cho 2n-1

2(3n+4)=6n+8=6n-3+11=3(2n-1)+11

Vậy để 3n+4 chia hết cho 2n-1 thì 11 phải chia hết cho 2n-1

=> Có 2 trường hợp:

+/ 2n-1=1 => n=1

+/ 2n-1=11 => n=6

ĐS: n={1;6}

Ta có : \(\frac{3n+5}{n+1}=\frac{3n+3+2}{n+1}=1+\frac{2}{n+1}\)

Vậy để Biểu thức trên có giá trị là một số tự nhiên

\(\Rightarrow n+1\inƯ\left(2\right)=\left(1;2\right)\)

\(\Rightarrow n\in\left(0;1\right)\)

Bài 2: 

a) Ta có: \(A=\dfrac{4}{n-1}+\dfrac{6}{n-1}-\dfrac{3}{n-1}\)

\(=\dfrac{4+6-3}{n-1}\)

\(=\dfrac{7}{n-1}\)

Để A là số tự nhiên thì \(7⋮n-1\)

\(\Leftrightarrow n-1\inƯ\left(7\right)\)

\(\Leftrightarrow n-1\in\left\{1;7\right\}\)

hay \(n\in\left\{2;8\right\}\)

Vậy: \(n\in\left\{2;8\right\}\)

ta có B=2n+9/n+2-3n+5n+1/n+2=4n+10/n+2                                                   Để B là STN thì 4n+10⋮n+2                          4n+8+2⋮n+2                                  4n+8⋮n+2                                                      ⇒2⋮n+2                                     n+2∈Ư(2)                                                        Ư(2)={1;2}                                  Vậy n=0                                                                                  

Ta có: =4+6−3n−1=4+6−3�−1

đặt 2n + 34 = a^2

34 = a^2-n^2

34=(a-n)(a+n)

a-n thuộc ước của 34 là { 1; 2; 17; 34} và a-n . Ta có bảng sau ( mik ko bt vẽ)

=>     a-n        1        2 

         a+n        34      17

        Mà tổng và hiệu 2 số nguyên cùng tính chẵn lẻ

      Vậy ....

Ta cóS = 14 +24 +34 +···+1004 không là số chính phương.

=>  S= (1004+14).100:2=50 900 ko là SCP

2: A=n^2+3n+2=(n+1)(n+2)

Để A là số nguyên tố thì n+1=1 hoặc n+2=2

=>n=0

Câu hỏi của Trương Anh Tú - Toán lớp 6 - Học toán với OnlineMath

Nếu n=0,suy ra A=0(thỏa mãn)

Nếu n=1 suy rs A=0(thỏa mãn)

Nếu n>1,ta có

A=n.(n^3-2.n^2+3n-2)

A=n.[n.(n^2-2n+3)-2]

A=n.[n.(n-1)^2+2.(n-1)]

A=n.(n-1).[n.(n-1)+2]

Ta thấy:[n.(n-1)]^2<A<[n.(n-1)+1]^2     (tự chứng minh)

Suy ra A không phải là số chính phương với n>1

                                Vậy n={0;1}

Bài 2: 

a: Để A là phân số thì \(n+4\ne0\)

hay \(n\ne-4\)

b: Để A là số tự nhiên thì \(3n-5⋮n+4\)

\(\Leftrightarrow-17⋮n+4\)

\(\Leftrightarrow n+4=17\)

hay n=13

3n + 4 thuoc BC(5.n-1) thi ta co 

3n-1+4=5

3n-1=5-4

3n-1=1

3n=1+1

3n=1

Nen n =2 

Vay 3n+4=32+4

va BC(5,n-1)=BC(5,2-1)

suy ra n=2

mình không hiểu câu này

ko bít