Tìm số nguyên tố p sao cho tồn tại số tự nhiên n để p=n3-n2+n-1

Những câu hỏi liên quan
Tìm số tự nhiên n để p là số nguyên tố biết : n3-n2+n-1
`P=n^3-n^2+n-1`
`=n^2(n-1)+(n-1)`
`=(n-1)(n^2+1)`
Vì n là stn thì p là snt khi
`n-1=1=>n=2`
Vậy n=2
Đúng 1
Bình luận (0)
Tìm Tìm số tự nhiên n để :
A=n3-n2+n-1 là số nguyên tố.
tìm số nguyên tố p sao cho tồn tại số tự nhiên n để p=n^3-n^2+n-1
p=
Tìm số nguyên tố p sao cho tồn tại số tự nhiên n để p=n3- n2 +n - 1
p = n3 - n2 + n - 1 = (n3 - n2) + (n - 1) = n2(n - 1) + (n - 1) = (n2 + 1)(n - 1)
Để p là số nguyên tố ta xét các trường hợp:
+) Nếu n - 1 = 1 => n = 2
=> p = (22 + 1)(2 - 1) = 5.1 = 5 là số nguyên tố.( thỏa mãn )
+) Nếu n > 3 => n - 1 > 2
và n2 + 1 > 10
=> p có nhiều hơn 2 ước => p là hợp số (loại)
Vậy n = 2 thì p là số nguyên tố
Cho mình 1` đúng nha
Đúng 0
Bình luận (0)
tìm số nguyên tố p sao cho tồn tại số tự nhiên n để p=\(n^3-n^2+n-1\) p là
Trl :
Bạn kia làm đúng rồi nhé !
Học tốt nhé bạn @
tìm số nguyên tố p sao cho tồn tại số tự nhiên n để \(p=n^3-n^2+n-1\)
dễ mà
n^3-n^2+n-1
=n^2(n-1)+(n-1)=(n-1)(n^2+1)
do p là snt nên p chỉ có 2 ước là 1 và chính nó=>n-1=1=>n=2
=>p=1(2^2+1)=5
vậy p=5
Đúng 0
Bình luận (0)
\(p=\)\(5\)nha bạn
Chúc các bạn học giỏi
Nha
Đúng 0
Bình luận (0)
dễ mà
n^3-n^2+n-1
=n^2(n-1)+(n-1)=(n-1)(n^2+1)
do p là snt nên p chỉ có 2 ước là 1 và chính nó=>n-1=1=>n=2
=>p=1(2^2+1)=5
vậy p=5
:3
Đúng 0
Bình luận (0)
Bài 1: Tìm n thuộc N* sao cho n3 - n2 + n - 1 là số tự nhiên
Bài 2: C/m nếu 2n - 1 (n > 2) là số nguyên tố thì 2n + 1 là hợp số
Bài 3: Cho m và m2 + 2 là số nguyên tố. C/m m3 + 2 cùng là số nguyên tố
1,
Đặt A = n3 - n2 + n - 1
Ta có A = n2(n - 1) + (n - 1) = (n - 1)(n2 + 1)
Vì A nguyên tố nên A chỉ có 2 Ư. Ư thứ 1 là 1 còn Ư thứ 2 nguyên tố nên ta suy ra 2 trường hợp :
TH1 : n - 1 = 1 và n2 + 1 nguyên tố
⇒
n = 2 và n2 + 1 = 5 nguyên tố (thỏa)
TH2 : n2 + 1 = 1 và n - 1 nguyên tố
⇒
n = 0 và n - 1 = - 1( ko thỏa)
Vậy n = 2
2 ,
Xột số A = (2n – 1)2n(2n + 1)
A là tích của 3 số tự nhiên liờn tiệp nên A ⋮ 3
Mặt khỏc 2n – 1 là số nguyên tố ( theo giả thiết )
2n không chia hết cho 3
Vậy 2n + 1 phải chia hết cho 3 ⇒ 2n + 1 là hợp số.
3 ,
Giải:
Với m=2 thì m2+2=4+2= 6 là hợp số (loại)
Với m=3 thì m2+2 = 9+2= 11 (thoải mãn)
Với m= 3k+1 ( với k ẻ N) thì: m2+2 = (3k+1)2 +2 = 3(3k2+2k+1) là hợp số ( loại)
Với m= 3k+2 thì: m2+2= (3k+2)2 +2 = 3(3k2+4k+2) là hợp số (loại)
Vậy với m= 3 thì m và m2+2 là số nguyên tố. Khi đó m3+ 2= 33+2 = 29 là số nguyên tố.
Xem thêm câu trả lời
Tìm n ∈ N * sao cho : n3 – n2 + n – 1 là số nguyên tố
Ta có :
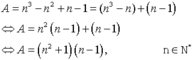
Nếu n = 1 suy ra A = 0
Nếu n = 2 suy ra A = 5 là số nguyên tố
Nếu n>2 thì A là tích của hai thừa số mà mỗi thừa số đều lớn hơn hai . Vậy A là hợp số
Vậy để A = n3 – n2 + n – 1 là số nguyên tố thì n = 2.
Đúng 0
Bình luận (0)
tìm số tự nhiên n sao cho p=(n-3)(n2 –n -1) là số nguyên tố






















