Câu 6: Cho tam giác ABC đều, cạnh bằng 5cm. Tỉnh các tích vô hưởng vec AB . vec AC vec AB . vec BC
Những câu hỏi liên quan
Câu 1: Cho tam giác đều ABC có cạnh là 10a, M là trung điểm của BC. Tính | vec AB + vec AM | ? vec AM . vec BA ? Câu 2: Cho tam giác ABC vuông tại A có AB = 2a căn 3 ; AC = 2a . Tính ? vec AB . vec BC ; | vec AB - vec AC |
Câu 2:
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=\left(2a\right)^2+\left(2a\sqrt{3}\right)^2=16a^2\)
=>BC=4a
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{1}{2}\)
nên \(\widehat{ABC}=30^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=60^0\)
Lấy điểm E sao cho \(\overrightarrow{AB}=\overrightarrow{BE}\)
=>B là trung điểm của AE
=>\(\widehat{CBE}+\widehat{CBA}=180^0\)(hai góc kề bù)
=>\(\widehat{CBE}=180^0-30^0=150^0\)
\(\overrightarrow{AB}\cdot\overrightarrow{BC}=\overrightarrow{BE}\cdot\overrightarrow{BC}\)
\(=BE\cdot BC\cdot cos\left(\overrightarrow{BE};\overrightarrow{BC}\right)\)
\(=2a\sqrt{3}\cdot4a\cdot cos150=-12a^2\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{AB}+\overrightarrow{CA}\right|=\left|\overrightarrow{CB}\right|=CB=4a\)
Đúng 1
Bình luận (0)
Câu 10: Cho tam giác ABC có AB = 2 BC = 4 , CA = 3 Tính vec GA . vec GB + vec GB . vec GC + vec GC . vec GA
giúp mik ba bài này với ^-^
1. Cho hình chữ nhật ABCD có AB 3a , AD 4a
a) Tính / vec tơ AD - vec tơ AB / b) Dựng vec tơ u vec tơ CA - vec tơ AB . Tính / vec tơ u /
2. Cho △ABC đều cạnh a . Gọi I là trung điểm BC
a) Tính / vec tơ AB - vec tơ AC / b) Tính / vec tơ BA - vec tơ BI /
3. Cho △ABC vuông tại A . Biết AB 6a , AC 8a . Tính / vec tơ AB - vec tơ AC /
Đọc tiếp
giúp mik ba bài này với ^-^
1. Cho hình chữ nhật ABCD có AB = 3a , AD = 4a
a) Tính / vec tơ AD - vec tơ AB / b) Dựng vec tơ u = vec tơ CA - vec tơ AB . Tính / vec tơ u /
2. Cho △ABC đều cạnh a . Gọi I là trung điểm BC
a) Tính / vec tơ AB - vec tơ AC / b) Tính / vec tơ BA - vec tơ BI /
3. Cho △ABC vuông tại A . Biết AB = 6a , AC = 8a . Tính / vec tơ AB - vec tơ AC /
Bài 4. Cho tam giác ABC có AM là đường trung tuyến và D là trung điểm của AM. a) Chứng minh rằng: 2 vec DA + vec DB + vec DC = vec 0 b) Chứng minh rằng: vec BD = 1 2 vec B vec A + 1 4 vec BC . c) Gọi E là điểm trên cạnh AC sao cho AE = 1/3 * A * C Chứng minh rằng B, D, E thẳng hàng. Tính tỉ số (DB)/(DE)
Cho tam giác ABC và M là trung điểm BC. Phân tích vec tơ AM theo vec tơ BA và vec tơ CA
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho . Hãy phân tích vec tơ theo hai vec tơ
Đọc tiếp
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho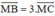 
. Hãy phân tích vec tơ 
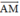theo hai vec tơ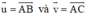 
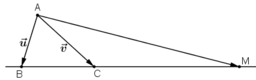
Ta có: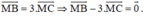 
Theo quy tắc ba điểm ta có:
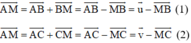
Lấy (1) trừ 3 lần (2) ta được:
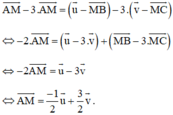
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn; BC = a, CA = b, AB = c và M là điểm thuộc miền trong của tam giác ABC sao cho các đường tròn ngoại tiếp các tam giác MBC, MCA, MAB bằng nhau. Chứng minh rằng:
\(\frac{1}{b^2+c^2-a^2}\vec{MA}+\frac{1}{c^2+a^2-b^2}\vec{MB}+\frac{1}{a^2+b^2-c^2}\vec{MC}=\vec{0}\)
Trong mặt phẳng xoy cho A (4;6) B(1;4) C(7;3/2) a tính độ dài các cạnh AB AC và BC của tam giác ABC B tính góc giữa hai vec tơ (AB BC) C chứng minh rằng tam giác ABC vuông tại A
\(a,AC=\sqrt{\left(4-7\right)^2+\left(6-\dfrac{3}{2}\right)^2}=\sqrt{9+\dfrac{81}{4}}=\dfrac{3\sqrt{13}}{2}\\ AB=\sqrt{\left(4-1\right)^2+\left(6-4\right)^2}=\sqrt{9+4}=\sqrt{13}\\ BC=\sqrt{\left(1-7\right)^2+\left(4-\dfrac{3}{2}\right)^2}=\sqrt{36+\dfrac{25}{4}}=\dfrac{13}{2}\)
Đúng 2
Bình luận (1)
\(c,BC^2=AB^2+AC^2\) nên \(\Delta ABC\) vuông tại A
Đúng 1
Bình luận (0)
mn ơi giúp mik với ,ai biết làm thì làm hết hộ mik nha còn ko làm hết được làm hộ mik 1 trong mấy
câu đó th T-T
1 Cho 8 điểm A , B, C, D , E , F , G ,H . CMR
vec tơ AC + vec to BF + vec tơ GD + vec tơ HE vec tơ AD + vec tơ BE + vec tơ GC + vec tơ HF
2 Cho tam giác ABC , từ A , B , C dựng 3 vec tơ tùy ý vec tơ AA , vec tơ BB , vec tơ CC
CMR : vec tơ AA + vec tơ BB + vec tơ CC vec tơ BA + vec tơ CB + vec tơ AC
3 Gọi O là tâm của hbh ABCD , CMR :
a) vec tơ DO + vec tơ AO vec tơ...
Đọc tiếp
mn ơi giúp mik với ,ai biết làm thì làm hết hộ mik nha còn ko làm hết được làm hộ mik 1 trong mấy
câu đó th T-T
1 Cho 8 điểm A , B, C, D , E , F , G ,H . CMR
vec tơ AC + vec to BF + vec tơ GD + vec tơ HE = vec tơ AD + vec tơ BE + vec tơ GC + vec tơ HF
2 Cho tam giác ABC , từ A , B , C dựng 3 vec tơ tùy ý vec tơ AA' , vec tơ BB' , vec tơ CC'
CMR : vec tơ AA' + vec tơ BB' + vec tơ CC' = vec tơ BA' + vec tơ CB' + vec tơ AC'
3 Gọi O là tâm của hbh ABCD , CMR :
a) vec tơ DO + vec tơ AO = vec tơ AB
b) vec tơ OD + vec tơ OC = vec tơ BC
c ) vec tơ OA + vec tơ OB + vec tơ OC + vec tơ OD = vec tơ 0
d) vec tơ MA + vec tơ MC = vec tơ MB + vec tơ MD ( với M là 1 điểm tùy ý )
help me
