
Những câu hỏi liên quan
Cho ABC có AB = AC , K là trung điểm của Bc . từ C kẻ đường vuông góc vs BC cắt AB tại E . chứng minh:
a, Tam giác ABK = Tam giác ACK
B, CE // AK
c, Trên nửa mặt phẳng bờ BC ko chứa điểm A kẻ tia KX //AC . Lấy I thuộc Kx sao cho KI = AB . Chứng minh 3 điểm I,C,E thẳng hàng
Cho tam giác ABC, K là trung điểm của BC. Trên nửa mặt phẳng bờ AC không chứa B kẻ tia Ax vuông góc với AC; trên tia Ax lấy điểm M sao cho AM=AC. Trên nửa mặt phẳng bờ AB không chứa điểm C, kẻ tia Ay vuông góc với AB; trên tia Ay lấy điểm N sao cho AN=AB. Lấy điểm P trên ta AK sao cho AK=KP.
a)Chứng minh AC=BP,
b) C/m: AC song song với BP.
Cho tam giác ABC, K là trung điểm của BC. Trên nửa mặt phẳng bờ AC không chứa B kẻ tia Ax vuông góc với AC; trên tia Ax lấy điểm M sao cho AMAC. Trên nửa mặt phẳng bờ AB không chứa điểm C, kẻ tia Ay vuông góc với AB; trên tia Ay lấy điểm N sao cho ANAB. Lấy điểm P trên ta AK sao cho AKKP.b) Chứng minh tam giác ABPtam giác NAM, AK vuông góc với MN.
Đọc tiếp
Cho tam giác ABC, K là trung điểm của BC. Trên nửa mặt phẳng bờ AC không chứa B kẻ tia Ax vuông góc với AC; trên tia Ax lấy điểm M sao cho AM=AC. Trên nửa mặt phẳng bờ AB không chứa điểm C, kẻ tia Ay vuông góc với AB; trên tia Ay lấy điểm N sao cho AN=AB. Lấy điểm P trên ta AK sao cho AK=KP.
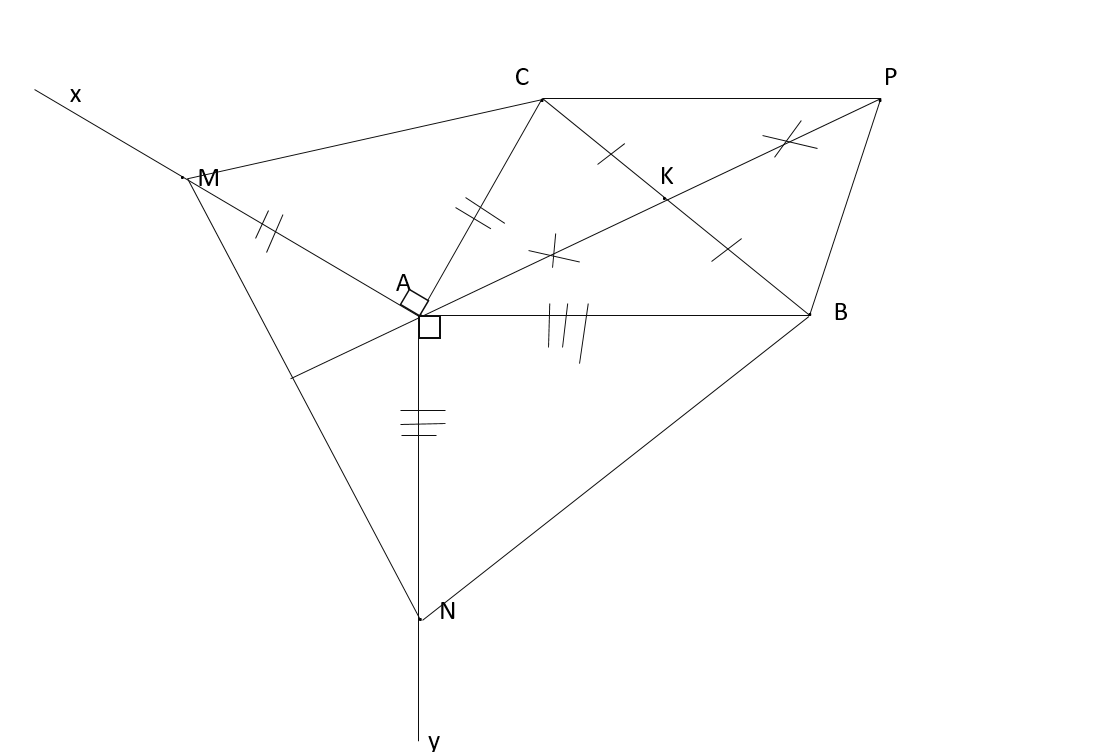
b) Chứng minh tam giác ABP=tam giác NAM, AK vuông góc với MN.
có ai giúp tui với thiên tài đâu hết r :))
Đúng 0
Bình luận (0)
Cho tam giác ABC, K là trung điểm của BC. Trên nửa mặt phẳng bờ AC không chứa B kẻ tia Ax vuông góc với AC; trên tia Ax lấy điểm M sao cho AMAC. Trên nửa mặt phẳng bờ AB không chứa điểm C, kẻ tia Ay vuông góc với AB; trên tia Ay lấy điểm N sao cho ANAB. Lấy điểm P trên ta AK sao cho AKKP.a)Chứng minh tam giác AKCtam giác PKB, và AC song song với BP.b) Chứng minh tam giác ABPtam giác NAM, AK vuông góc với MN.
Đọc tiếp
Cho tam giác ABC, K là trung điểm của BC. Trên nửa mặt phẳng bờ AC không chứa B kẻ tia Ax vuông góc với AC; trên tia Ax lấy điểm M sao cho AM=AC. Trên nửa mặt phẳng bờ AB không chứa điểm C, kẻ tia Ay vuông góc với AB; trên tia Ay lấy điểm N sao cho AN=AB. Lấy điểm P trên ta AK sao cho AK=KP.
a)Chứng minh tam giác AKC=tam giác PKB, và AC song song với BP.
b) Chứng minh tam giác ABP=tam giác NAM, AK vuông góc với MN.
Cho tam giác ABC nhọn. Trên nửa mặt phẳng bờ AB, không chứa điểm C, lấy điểm D sao cho AD vuông góc AB; AD=AB. Trên nửa mặt phẳng bờ AC, không chứa điểm B, lấy điẻm E sao cho AE vuông góc AC; AE=AC. Kẻ AH vuông góc BC, tia HA cắt DE tại K. Chứng minh rằng K là trung điểm của DE.
Dùng hình của bạn Mai nhé.
Kẽ DP và EQ \(⊥\)HK tại P và Q.
Xét \(\Delta DPA\)và \(\Delta AHB\)có
\(\hept{\begin{cases}\widehat{DPA}=\widehat{AHB}=90\\DA=AB\\\widehat{PDA}=\widehat{HAB}\left(phu\widehat{PAD}\right)\end{cases}}\)
\(\Rightarrow\Delta DPA=\Delta AHB\)
\(\Rightarrow DP=AH\left(1\right)\)
Xét \(\Delta EQA\)và \(\Delta AHC\)có
\(\hept{\begin{cases}\widehat{EQA}=\widehat{CHA}=90\\EA=CA\\\widehat{QEA}=\widehat{HCA}\left(phu\widehat{QAE}\right)\end{cases}}\)
\(\Rightarrow\Delta EQA=\Delta AHC\)
\(\Rightarrow EQ=AH\left(2\right)\)
Từ (1) và (2) \(\Rightarrow DP=EQ\)
Xét \(\Delta DPK\)và \(\Delta EQK\)có
\(\hept{\begin{cases}\widehat{DPK}=\widehat{EQK}=90\\DP=EQ\\\widehat{DKP}=\widehat{EKQ}\end{cases}}\)
\(\Rightarrow\Delta DPK=\Delta EQK\)
\(\Rightarrow DK=EK\)
Vậy K là trung điểm của DE
Đúng 1
Bình luận (0)
Hình xấu quá anh thông cảm. Anh đọc lại đề để tránh bị lộn kí hiệu góc vuông nha anh :)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 5:(2,5đ) Cho ABC cân tại A, từ A kẻ AK vuông góc với BC tại K a) Chứng minh: ABK =ACK b) Trên tia đối của tia KA lấy điểm D sao cho KA= KD. Chứng minh AC=DC c) Qua K kẻ đường thẳng song song với AC cắt AB tại M.Chứng minh M là trung điểm AB
a: Xét ΔAKB vuông tại K và ΔAKC vuông tại K có
AB=AC
AK chung
=>ΔAKB=ΔAKC
b: Xet ΔCAD có
CK vừa là đường cao, vừa là trung tuyến
=>ΔCAD cân tại C
=>CA=CD
c: Xét ΔABC có
K là trung điểm của CB
KM//AC
=>M là trung điểm của AB
Đúng 0
Bình luận (0)
Cho tam giác AB nhọn. Trên nửa mặt phẳng bờ ABD, không chứa điểm D, lấy điểm C sao cho AC vuông góc AB; AC=AB. Trên nửa mặt phẳng bờ D, không chứa điểm B, lấy điẻm E sao cho AE vuông góc AD; AE=AD. Kẻ AH vuông góc BC, tia HA cắt CE tại K. Chứng minh rằng K là trung điểm của CE.
Cho tam giác ABC nhọn. Trên nửa mặt phẳng bờ AB, không chứa điểm C, lấy điểm D sao cho AD vuông góc AB; AD=AB. Trên nửa mặt phẳng bờ AC, không chứa điểm B, lấy điẻm E sao cho AE vuông góc AC; AE=AC. Kẻ AH vuông góc BC, tia HA cắt DE tại K. Chứng minh rằng K là trung điểm của DE
Câu hỏi của Nguyễn Đức Hiếu - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\) nhọn . Trên nửa mặt phẳng bờ AB , không chưa điểm C , lấy điểm D sao cho AD vuông góc AB ; AD = AB . Trên nửa mặt phẳng bờ AC , không chứa điểm B , lấy E sao cho AE vuông góc AC . Kẻ AH vuông góc BC , tia HA cắt DE tại K . Chứng minh K là trung điểm DE
Câu hỏi của Nguyễn Đức Hiếu - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.
Đúng 0
Bình luận (0)















