Tam giác ABC có độ dài các cạnh là 24cm; 32cm; 40cm có phải là tam giác vuông ko? Vì sao?? Giúp mình dc ko??

Những câu hỏi liên quan
Giúp mình bài này nhé!!!
Tam giác ABC có độ dài các cạnh là 24cm; 32cm; 40cm có phải là tam giác vuông ko? Vì sao??
Ta có:
24^2+32^2=1600
40^2=1600
=>24^2+32^2=40^2
=>Tam giác đó là tam giác vuông(Theo định lí talet đảo)
Đúng 0
Bình luận (0)
Giả sử AB=24
AC=32
BC=40
Ta có:40^2=1600
24^2=576
32^2=1034
=>Ta đc:1600=576+1034
=>BC^2=AB^2+AC^2
=>tam giác này là tam giác vuông
Đúng 0
Bình luận (0)
Đây lak tam giác vuông vì 24^2+32^2=40^2
Anh Khánh ơi cái này là định lí Pytago đảo! ~o~
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB=18cm, AC=24cm
1.Tính độ dài cạnh BC
2.Gọi I là trung điểm của BC. Đường vuông góc với cạnh BC tại I cắt AC tại E. Chứng minh rằng
a) Hai tam giác ABC và IEC đồng dạng
b) Tính độ dài các cạnh của tam giác IEC
1: \(BC=\sqrt{18^2+24^2}=30\left(cm\right)\)
2: Xét ΔABC vuông tại A và ΔIEC vuông tại I có
góc C chung
=>ΔABC đồng dạng với ΔIEC
b:
IC=BC/2=15cm
ΔABC đồng dạng với ΔIEC
=>AB/IE=BC/EC=AC/IC
=>18/IE=30/EC=24/15=8/5
=>IE=11,25cm; EC=18,75cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB=18cm, AC=24cm
1.Tính độ dài cạnh BC
2.Gọi I là trung điểm của BC. Đường vuông góc với cạnh BC tại I cắt AC tại E. Chứng minh rằng
a) Hai tam giác ABC và IEC đồng dạng
b) Tính độ dài các cạnh của tam giác IEC
1: \(BC=\sqrt{18^2+24^2}=30\left(cm\right)\)
2: Xét ΔABC vuông tại A và ΔIEC vuông tại I có
góc C chung
=>ΔABC đồng dạng với ΔIEC
b:
IC=BC/2=15cm
ΔABC đồng dạng với ΔIEC
=>AB/IE=BC/EC=AC/IC
=>18/IE=30/EC=24/15=8/5
=>IE=11,25cm; EC=18,75cm
Đúng 2
Bình luận (0)
Hình tam giác ABC có độ dài cạnh đáy là 24cm. Chiều cao bằng 2/3 cạnh đáy . Tính diện tích tam giác đó.
Chiều cao hình tam giác ABC là :
24 x 2/3 = 16 ( cm )
Diện tích tam giác ABC là :
24 x 16 : 2 = 192 ( cm2)
Đáp số : 192 cm2
Đúng 0
Bình luận (0)
Chiều cao của hình tam giác là :
24 : 3 x 2 = 16 cm
Diện ích của hình tam giác là :
24 x 16 = 384 cm2
Đáp số 384 cm2
Đúng 0
Bình luận (0)
chiều cao : 24><2:3=16(cm)
S tam giác:1/2><24><16=192(cm vuông)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đường cao AH=24cm. Biết AB:AC=3:4. Tính độ dài các cạnh của tam giác ABC.
Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{4}\)
nên \(AB=\dfrac{3}{4}AC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{9}{16}AC^2}+\dfrac{1}{AC^2}=\dfrac{1}{576}\)
\(\Leftrightarrow AC^2\cdot\dfrac{9}{16}=576\cdot\dfrac{25}{16}=900\)
\(\Leftrightarrow AC^2=1600\left(cm\right)\)
\(\Leftrightarrow AC=40\left(cm\right)\)
\(\Leftrightarrow AB=30\left(cm\right)\)
\(\Leftrightarrow BC=50cm\)
Đúng 0
Bình luận (0)
Tam giác ABC có độ dài các cạnh AB = 24cm, AC = 30cm, BC = 36cm. Trên cạnh AB lấy điểm M sao cho AM =20cm, trên cạnh AC lấy điểm N sao cho AN =16 cm. Chứng minh tam giác ANM đồng dạng với tam giác ABC và tính MN
Xét ΔANM và ΔABC có
AN/AB=AM/AC
\(\widehat{NAM}\) chung
Do đó: ΔANM\(\sim\)ΔABC
Đúng 0
Bình luận (1)
Tam giác ABC có cạnh AB=24cm, cạnh AC=30cm.Một đường gấp khúc MENDPC chia tam giác ABC thành sáu tam giác có diện tích bằng nhau(đó là các tam giác AME,MEN,END,NDP,DPC và PCB).Các điểm M,N,P ở trên cạnh AB;các điểm E,D ở trên cạnh AC.Tính độ dài các đoạn thẳng AM,AN,AP,AE,AD
Giúp mình nhanh nha,giải chi tiết
Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không? Tại sao?a) 24cm, 21cm, 27cm và 28dm, 36dm, 32dm.b) Tam giác ABC và tam giác DEF có
A
B
3
B
C
4
C
A
5
v
à
D
E
6...
Đọc tiếp
Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không? Tại sao?
a) 24cm, 21cm, 27cm và 28dm, 36dm, 32dm.
b) Tam giác ABC và tam giác DEF có A B 3 = B C 4 = C A 5 v à D E 6 = F D 9 = E F 8 .
Sắp xếp các cạnh của mỗi tam giác theo thứ tự tăng dần rồi mới lập tỉ số, ta được hai tam giác đã cho đồng dạng.
b) Đặt 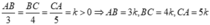
Đặt 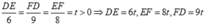
Lập tỉ số các cặp cạnh tương ứng, dẫn tới kết luận hai tam giác không đồng dạng.
Đúng 0
Bình luận (0)
Câu 3. Cho ABC có AB 18cm , AC 24cm , BC 30cm. Gọi M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với AB cắt AC, AB lần lượt tạo D và E.a) Chứng minh rằng: tam giác ABC đồng dạng với tam giác MDC.b) Tính độ dài các cạnh MDC.c) Tính độ dài BE , EC.Câu 4. Cho hình chóp tứ giác đều SABCD ; ABCD là hình vuông cạnh 20cm, cạnh bên 24cm. Tính thể tích hình chóp.
Đọc tiếp
Câu 3. Cho ABC có AB = 18cm , AC = 24cm , BC = 30cm. Gọi M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với AB cắt AC, AB lần lượt tạo D và E.
a) Chứng minh rằng: tam giác ABC đồng dạng với tam giác MDC.
b) Tính độ dài các cạnh MDC.
c) Tính độ dài BE , EC.
Câu 4. Cho hình chóp tứ giác đều SABCD ; ABCD là hình vuông cạnh 20cm, cạnh bên 24cm. Tính thể tích hình chóp.
a, Xét tam giác ABC có:
AC2+AB2=242+182=900=302=BC2AC2+AB2=242+182=900=302=BC2⇒⇒ Tam giác ABC vuông tại A
Xét tam giác ABC và MDC có:
DMCˆ=BACˆDMC^=BAC^
CˆC^ là góc chung
⇒⇒ Tam giác ABC ~MDC ( g.g)
b, Vì tam giác ABC~MDC ⇒ABAC=MDMC=34⇒MD=3MC4⇒ABAC=MDMC=34⇒MD=3MC4ACBC=MCDC=45⇒DC=5MC4ACBC=MCDC=45⇒DC=5MC4
Mà:
ABMD=BCDC=ACMC=AB+BC+ACMD+DC+MC=723MC4+5MC4+4MC4ABMD=BCDC=ACMC=AB+BC+ACMD+DC+MC=723MC4+5MC4+4MC4=7212MC3⇒12MC=72.3=216⇒MC=18cm=7212MC3⇒12MC=72.3=216⇒MC=18cm⇒MD=3.184=13,5cm⇒MD=3.184=13,5cm
⇒DC=5.184=22,5cm


















