Xác định hàm số y = ax + b có đồ thị (D) biết (D) // (D’) : y = −3x + 2 và đi qua 𝑀(3 ; 0).

Những câu hỏi liên quan
Cho hàm số y=-2x+1 (d)
a) Vẽ đồ thị (d) của hàm số y=-2x+1
b) Xác định các hệ số a và b của hàm số y=ax+b, biết rằng đồ thị của hàm số này song song với đồ thị (d) và đi qua điểm A(2;1).
b: Vì (d1)//(d) nên (d1): y=-2x+b
=>a=-2
Thay x=2 và y=1 vào (d1), ta được:
b-4=1
=>b=5
a: 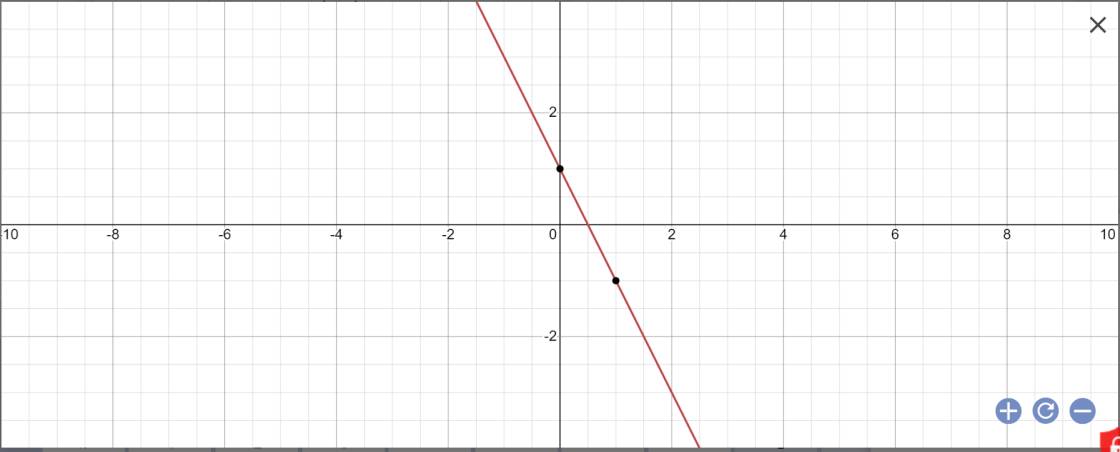
Đúng 1
Bình luận (0)
Xác định hàm số bậc nhất y= ax+b ,biết
a, hệ số góc bằng 2 và đồ thị hàm số đi qua A( 1;2)
b,đồ thị hàm số đi qua điểm A(-2;2) và cắt đường thẳng (d) y=-2x+4 tại điểm có hoành độ bằng 3
a) Hệ số góc bằng 2
=> a=2
Đồ thị hàm số đi qua A (1; 2)
=> 2=a.1+b<=> 2=2.1+b <=> b=0
Vậy hàm số: y=2x
b)
+) Đồ thị hàm số đi qua điểm A (-2; 2)
=> 2=a. (-2)+b <=> -2a+b=2 (1)
+) Đồ thị hàm số cắt đường thẳng (d) y=-2x+4 tại điểm có hoành độ bằng 3
Gọi điểm đó là: B(3; y)
(d) qua B(3; y) => y=-2.3+4=-2
=> B(3; -2)
đồ thị hàm số qua B => -2=a.3+b <=> 3a+b=-2 (2)
Từ (1); (2) ta có:a=-4/5, b=2/5
Vậy: y=-4/5 x+2/5
Đúng 0
Bình luận (0)
Xác định dạng của hàm số (d) y=ax+b biết đồ thị hàm số đi qua A(4;9) và B(1;9/2)
đồ thị có dạng \(y=ax+b\)
đồ thị đi qua A(4;9) suy ra \(4a+b=9\)(1)
đồ thị đi qua 8(1;9;2) suy ra \(a+b=\frac{9}{2}\)-> b= \(\frac{9}{2}-a\)(2)
thay (2) vào (1) ta có \(4a+\frac{9}{2}-a=9\)-> a=\(\frac{3}{2}\); b= 3
đồ thị cần tìm là \(y=\frac{3}{2}x+3\)
Đúng 0
Bình luận (0)
Xác định hàm số y=ax+b biết:
a/ Đồ thị hàm số đi qua 2 điểm A(1;5) B(2;-3)
b/Đồ thị hàm số // (d'): y= -2x-1 đi qua điểm C(1/2;4)
1) Vẽ đồ thị (d) của hàm số y = 2x – 3
2) Tìm tọa độ giao điểm của (d) và (d1) y = - 3x + 2 bằng phép tính.
3) Xác định các hệ số a và b của hàm số y = ax + b, biết rằng đồ thị (d2) của hàm số
này cắt trục tung tại điểm có tung độ là -2 và (d), (d1), (d2) đồng quy.
2: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-3=-3x+2\\y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xác định hàm số y=ax+b.Biết đồ thị hàm số:
a)Đi qua điểm A(1;2)vuông góc với đồ thị hàm số \(y=\dfrac{1}{3}x-1\)
b)Là đường thẳng (d) đi qua 2 điểm B(0;-1) và C(3;0).Vẽ (d) và tính góc \(\alpha\) của (d) với trục hoành
a) Vì đồ thị hàm số y=ax+b vuông góc với đồ thị hàm số \(y=\dfrac{1}{3}x-1\) nên \(a\cdot\dfrac{1}{3}=-1\)
\(\Leftrightarrow a=-1:\dfrac{1}{3}=-1\cdot\dfrac{3}{1}=-3\)
Vậy: Hàm số có dạng y=-3x+b
Vì đồ thị hàm số y=-3x+b đi qua điểm A(1;2) nên
Thay x=1 và y=2 vào hàm số y=-3x+b, ta được:
\(-3\cdot1+b=2\)
\(\Leftrightarrow b-3=2\)
hay b=5
Vậy: Hàm số có dạng y=-3x+5
Đúng 2
Bình luận (0)
a) Vẽ đồ thị (D) của hàm số\(y=1-\frac{3}{2}x\) trên hệ trục tọa độ
b) gọi M là giao điểm của (D) và trục tung Oy (x=0).Xác định a và b của hàm số y=ax+b có đồ thị (d), biết (d) đi qua điểm M và điểm N(2;3)
b: Tọa độ M là:
x=0 và y=1-3/2*0=1
Vì (d) đi qua M(0;1) và N(2;3) nên ta có hệ:
0a+b=1 và 2a+b=3
=>b=1; a=1
Đúng 0
Bình luận (0)
xác định hệ số a,b của hàm số y=ax+b, biết đồ thị (d) của hàm số đi qua điểm A (2;-2) và song song với đường thẳng y=1/2x + 1
Lời giải:
$(d)$ song song với $y=\frac{1}{2}x+1$ nên $a=\frac{1}{2}$
$A\in (d)$ nên:
$y_A=ax_A+b$
$\Leftrightarrow -2=a.2+b$
$\Leftrightarrow -2=\frac{1}{2}.2+b$
$\Leftrightarrow b=-3$
Vậy $a=\frac{1}{2}; b=-3$
Đúng 0
Bình luận (0)














