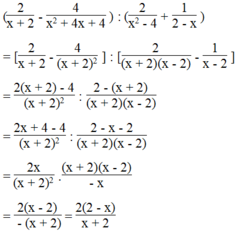THỰC HIỆN PHÉP TÍNH (4x^2-4x+48):(x+4)

Những câu hỏi liên quan
Thực hiện phép tính:
a) 4x+13/5x(x-7) - x-48/5x(7-x)
b) 2x2-4x+2/4x+4 . x2-1/(x-1)3
c) x2+1/x+1 + 2x/x+1
d) x2+1/x-1 - 2x/x-1
Cảm ơn mng !!!
Thực hiện các phép tính sau:
2
x
+
2
-
4
x
2
+
4
x
+
4
:
2
x
2...
Đọc tiếp
Thực hiện các phép tính sau: 2 x + 2 - 4 x 2 + 4 x + 4 : 2 x 2 - 4 + 1 2 - x
Thực hiện phép tính
a) (-x3+2x4-4-x2+7x):(x2+x-1)
b) y phần 2x2-xy + 4x phần y2-2xy
c) 6x+48 phần 7x-7 : x2-64 phần x2-2x+1
a: \(\dfrac{2x^4-x^3-x^2+7x-4}{x^2+x-1}\)
\(=\dfrac{2x^4+2x^3-2x^2-3x^3-3x^2+3x+4x^2+4x-4}{x^2+x-1}\)
=2x^2-3x+4
b: \(=\dfrac{y}{x\left(2x-y\right)}+\dfrac{4x}{y\left(y-2x\right)}\)
\(=\dfrac{y^2-4x^2}{xy\left(2x-y\right)}=\dfrac{-\left(2x-y\right)\left(2x+y\right)}{xy\left(2x-y\right)}=\dfrac{-2x-y}{xy}\)
c: \(=\dfrac{6\left(x+8\right)}{7\left(x-1\right)}\cdot\dfrac{\left(x-1\right)^2}{\left(x-8\right)\left(x+8\right)}=\dfrac{6\left(x-1\right)}{7\left(x-8\right)}\)
Đúng 0
Bình luận (0)
Thực hiện các phép tính sau a) 3y/28^2 . 2x/7y^4.49x^4y^3 b) (-20x/3y^2) : (-4x^3/5y) c) 4x+12/(x+4)^2 : 3(x+3)/x+4
\(\dfrac{6\left(4-4x+x^2\right)}{x^3y}:\dfrac{x-2}{x^3y^2}\)
Thực hiện phép tính
\(=\dfrac{6\left(x-2\right)^2}{x^3y}\cdot\dfrac{x^3y^2}{x-2}=6\left(x-2\right)\cdot y\)
Đúng 1
Bình luận (0)
Câu 12. Thực hiện phép tính 25. 68 + 68. 75. 4, kết quả là:A.12 200 B.22 100 C.6804 D.27 200Câu 13. Tìm x biết 4x - 12 48, ta được x bằng:A.32 B.9 C.15 D.54Câu 14. Tìm x biết 2346 : (x - 8) 23, ta được x bằng:A110 B.92 C.93 D.94
Đọc tiếp
Câu 12. Thực hiện phép tính 25. 68 + 68. 75. 4, kết quả là:
A.12 200 B.22 100 C.6804 D.27 200
Câu 13. Tìm x biết 4x - 12 = 48, ta được x bằng:
A.32 B.9 C.15 D.54
Câu 14. Tìm x biết 2346 : (x - 8) = 23, ta được x bằng:
A110 B.92 C.93 D.94
Câu 12: B
Câu 13: C
Câu 14: A
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Thực hiện phép tính
(X^4-x^3+2x^2+4x) : (x^4-2x+4)
Giúp mik với. Thanks nhiều nha!
Xem chi tiết
ban chia đa thức 1 biến đã sắp xếp nha
Đúng 0
Bình luận (1)
ban chia đa thức 1 biến đã sắp xếp nha
Đúng 0
Bình luận (0)
thực hiện phép tính :
b ( x + 2 ) ( x^2 - 2x + 4 )
c ( 4x^ - 8x^2 + 13x - 5 ) : ( 2x -1 )
b. (x + 2)(x2 - 2x + 4)
= x3 - 2x2 + 4x + 2x2 - 4x + 8
= x3 + 8
Đúng 0
Bình luận (0)
c: \(\dfrac{4x^3-8x^2+13x-5}{2x-1}=\dfrac{4x^3-2x^2-6x^2+3x+10x-5}{2x-1}\)
=2x^2-3x+5
Đúng 0
Bình luận (0)
thực hiện phép tính\(\left(\frac{1}{x^2+4x+4}-\frac{1}{X^2-4x+4}\right)\div\left(\frac{1}{x+2}+\frac{1}{x-2}\right)\)
Ta có \(\left(\frac{1}{x^2+4x+4}-\frac{1}{x^2-4x+4}\right):\left(\frac{1}{x+2}+\frac{1}{x-2}\right)\)
\(=\frac{\left(x-2\right)^2-\left(x+2\right)^2}{\left(x-2\right)^2\left(x+2\right)^2}:\frac{x-2+x+2}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{\left(x-2+x+2\right)\left(x-2-x-2\right)}{\left(x-2\right)^2\left(x+2\right)^2}:\frac{2x}{\left(x+2\right)\left(x-2\right)}\)
\(\frac{-4.2x}{\left(x+2\right)^2\left(x-2\right)^2}.\frac{\left(x+2\right)\left(x-2\right)}{2x}=\frac{-4}{\left(x+2\right)\left(x-2\right)}\)
Đúng 0
Bình luận (0)