cho tam giác ABC biết AB=14cm AC=35cm đường phân giác AD bằng 12cm diện tích tam giác ABC là

Những câu hỏi liên quan
cho tam giác ABC , biết AB=14cm,AC=35cm,đường phân giác AD bằng 12cm . Diện tích tam giác ABC là ?
Kẻ DE//AB. BD/CD = AE/EC = AB/AC => AE/(EC+AE) = AB/(AB+AC) <=> AE = 10
^BAD = ^ADE (so le trong) => T/g ADE cân tại E
Kẻ EH vuông góc với AD => AH = 1/2 AD = 6. Theo đ/l Py-ta-go tính được EH = 8
=> S(ADE) = 48
S(ADE)/S(ADC) = AE/AC = 5/7 => S(ADC) = 67,2
S(ABD)/S(ADC) = BD/CD = 35/14 = 5/2 => S(ABD) = 168
=> S(ABC) = 235,2 (cm^2)
Đúng 0
Bình luận (0)
rffdhzhdfhdfxcgbdfdfdfdfdfdfdfdfdfgvdfxgvbfvzgdgdzxgzdgzdgzdddddddddddddddxfxzgggggggzffzdssssssss
Đúng 0
Bình luận (0)
cho tam giác ABC có AB=35CM ; AC=14cm ; đường phân giác AD=12cm Tinh diện tích tam giac ABC
Kẻ DE//AB. BD/CD = AE/EC = AB/AC => AE/(EC+AE) = AB/(AB+AC) <=> AE = 10
^BAD = ^ADE (so le trong) => T/g ADE cân tại E
Kẻ EH vuông góc với AD => AH = 1/2 AD = 6. Theo đ/l Py-ta-go tính được EH = 8
=> S(ADE) = 48
S(ADE)/S(ADC) = AE/AC = 5/7 => S(ADC) = 67,2
S(ABD)/S(ADC) = BD/CD = 35/14 = 5/2 => S(ABD) = 168
=> S(ABC) = 235,2 (cm^2)
Đúng 0
Bình luận (0)
Cho tam giác ABC,biết AB=14cm,AC=35cm,đường phân giác AD bằng 12cm.Diện tích tam giác ABC là
tính diện tích tam giác ABC,biết rằng AB=14cm,AC=35cm,đường phân giác AD =12
vẽ: DE//AB, ta có: \(\frac{AE}{EC}=\frac{DB}{BC}=\frac{AB}{AC}\)
thay vào AE/EC ta có: \(\frac{AE}{EC}=\frac{14}{35}\)
đặt AE = x thì EC = 35 - x, thay vao đăng thức, ta có:
\(\frac{x}{35-x}=\frac{14}{35}\)
\(\Rightarrow490-14x=35x\)
\(\Rightarrow x=10\)
trong tam giác AED cân tại E vẽ đường cao EH.
=> EH là đường trung tuyến nên AH = 6.
áp dụng ĐL pi-ta-go vào tam giác vuông AHE.
\(\Rightarrow EH=8\text{ nen }S_{\text{tam giác }}ADE=48cm^2\)
do tam giác ADE và DCE có chung đường cao nên SDEC = 120 cm2
\(\Rightarrow\orbr{\begin{cases}S_{ADC}=168cm^2\\S_{ABC}=235,2cm^2\end{cases}}\)
Đúng 0
Bình luận (0)
câu 1: Cho tam giác ABC , đường cao AH , H thuộc cạnh BC . Biết AB = 15cm, AC = 41cm, BH = 12cm. Tính diện tích tam giác ABC
câu 2 : Cho hình chữ nhật ABCD có AD = 14cm, BD = 50cm, O là giao điểm của hai đường chéo. Gọi E, F, G, H theo thứ tự là trung điểm của OA, OB, OC. Tính diện tích tứ giác EFGH
câu 3: Cho tam giác ABC , AH = AC = 10cm, BC = 12cm . Tính đường cao BK
làm nhanh giúp mình với
Tam giác ABC có AB= 12cm, AC = 20cm, BC= 28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E ∈ AC). Cho biết diện tích tam giác ABC là S,tính diện tích các tam ABD, ADE, DCE
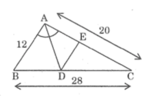
Vì △ ABD và △ ABC có chung đường cao kẻ từ đỉnh A nên:
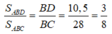
Vậy: S A B D = 3/8.S
S A D C = S A B C - S A B D = S - 3/8.S = 8/8.S - 3/8.S = 5/8.S
Vì DE // AB và AD là đường phân giác góc A nên AE = DE
Ta có: 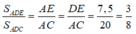
Vậy: 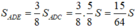
Ta có: 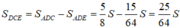
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 12cm, AC = 16cm. Kẻ đường cao AH và đường phân giác AD của góc BAC.
a. Cm: tam giác HBA ~ tam giác ABC
b. Tìm tỉ số diện tích tam giác ABD và tam giác ADC
c. Tính diện tích tam giác AHD
a) Xét ΔHBAΔHBA và ΔABCΔABC có:
ˆAHB=ˆCAB=90∘AHB^=CAB^=90∘
ˆBB^ là góc chung
⇒ΔHBA∼ΔABC⇒ΔHBA∼ΔABC (g-g)
c) ΔABCΔABC có ADAD là đường phân giác, theo tính chất đường phân giác ta có:
SΔABD=12⋅AH⋅BDSΔABD=12·AH·BD
⇒SΔABDSΔACD=BDDC=34⇒SΔABDSΔACD=BDDC=34

Đúng 3
Bình luận (3)
c, định lí Py-ta-go trong tam giác vg ABC (vg tại A)
BC^2= AB^2 +AC^2
BC=20 cm
Có HBA~ABC(cmt)
BH/AB=BA/BC
AB^2=BH*BC
BH=7,2 cm
CH=BC-BH=12,8 cm
xét ABH và CAH
ABH ~ CAH (g-g)
AH/CH=BH/AH
AH^2=BH*CH=7,2*12,8=92,16cm
AH=9,6 cm
ta có AD là tia pg
DB/AB=DC/AC=DB+DC/AB+AC=BC/AB+AC=5/7
DC=5/7*16= 11,4 cm
HD=HC-DC=1,4 cm
SAHD= AH*HD= 9,6*1,4=13,44 cm^2
Đúng 2
Bình luận (1)
Cho tam giác ABC có AB=14cm, AC=14cm, BC=12cm. Đường phân giác của góc BAC cắt BC ở D
a) Tính độ dài DB và DC
b) Tính tỉ số diện tích của hai tam giác ABD và ACD
c) Qua D kẻ đường thẳng song song với AB cắt cạnh AC ở E. Tính DE, AE, EC
a: ΔABC cân tại A
mà AD là phân giác
nên D là trung điểm của BC
=>DB=DC=6cm
b: Xét ΔADB và ΔADC có
AD chung
góc BAD=góc CAD
AB=AC
=>ΔADB=ΔADC
=>\(\dfrac{S_{ADB}}{S_{ADC}}=1\)
c: Xet ΔCAB có DE//AB
nên DE/AB=CD/CB=1/2
=>DE=7cm
DE//AB
=>CE/CA=CD/CB
=>CE/14=1/2
=>CE=7cm
=>AE=7cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=14cm, AC=13cm, BC=12cm. Đường phân giác của góc BAC cắt BC ở Da) Tính độ dài DB và DCb) Tính tỉ số diện tích của hai tam giác ABD và ACD giúp tớ với ạ
a: Xét ΔABC có AD là phân giác
nên \(\frac{BD}{AB}=\frac{CD}{AC}\)
=>\(\frac{BD}{14}=\frac{CD}{13}\)
mà BD+CD=BC=12cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{BD}{14}=\frac{CD}{13}=\frac{BD+CD}{14+13}=\frac{12}{27}=\frac49\)
=>\(\begin{cases}BD=14\cdot\frac49=\frac{56}{9}\left(\operatorname{cm}\right)\\ CD=13\cdot\frac49=\frac{52}{9}\left(\operatorname{cm}\right)\end{cases}\)
b: Vì \(\frac{BD}{14}=\frac{CD}{13}\)
nên \(\frac{BD}{CD}=\frac{14}{13}\)
=>\(\frac{S_{ABD}}{S_{ACD}}=\frac{14}{13}\)
Đúng 0
Bình luận (0)





















