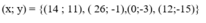x^2 + x+13 = y^2

Những câu hỏi liên quan
Tìm giá trị của x và y biết
1) x + y =10 và x= y. 2) 2.x + 3.y = 180 và x= y
3) x +y = 180 và x=y. 4) 3. x +5.y = 13 và y = 2.x
5) 3.x + 5.y = 13 và y = x + 1. 6) x+ y = 90 và x =2y
1) \(x+y=10\) mà \(x=y\) nên: \(x=y=\dfrac{10}{2}=5\)
2) \(2x+3y=180\) mà \(x=y\)
Ta có: \(2y+3y=180\Rightarrow5y=180\Rightarrow y=180:5=36\)
Vậy \(x=y=36\)
3) \(x+y=180\) mà \(x=y\) nên: \(x=y=\dfrac{180}{2}=90\)
4) \(3x+5y=13\) mà \(y=2x\) ta có:
\(3x+5\cdot2x=13\Rightarrow13x=13\Rightarrow x=1\)
\(y=2x=2\cdot1=2\)
Các câu còn lại bạn làm tương tự
Đúng 3
Bình luận (0)
Tìm y biết:
a. y – 6 : 2 – ( 48 – 24 x 2 : 6 – 3) = 0
b. (7 x 13 + 8 x 13) : ( 9 2 3 – y) = 39
a. Tính đúng y = 40
b. Tính đúng y = 4 2 3
Đúng 0
Bình luận (0)
a)| 4.x - 7 | = 13
b)| 1-2.x| =9
c) ( x^2 + 5).( x^2 - 36)
d) ( 2.x -1 ).(y+3)=11
e) ( 5-2.x ).(2.y+1)=13
a) |4x - 7| = 13
=> \(\orbr{\begin{cases}4x-7=13\\4x-7=-13\end{cases}}\)
=> \(\orbr{\begin{cases}4x=20\\4x=-6\end{cases}}\)
=> \(\orbr{\begin{cases}x=5\\x=-\frac{3}{2}\end{cases}}\)
b) tương tự)
Đúng 0
Bình luận (0)
d) Ta có: 11 = 1. 11 = 11. 1
Lập bảng:
| 2x - 1 | 1 | 11 | -1 | -11 |
| y + 3 | 11 | 1 | -11 | -1 |
| x | 1 | 6 | 0 | -5 |
| y | 8 | -2 | -14 | -4 |
Vậy ...
e) tương tự
Đúng 0
Bình luận (0)
\(\left|4x-7\right|=13\)
\(\Leftrightarrow\orbr{\begin{cases}4x-7=13\\4x-7=-13\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}4x=20\\4x=-6\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=5\\x=-\frac{6}{4}\end{cases}}\)
\(\left|1-2x\right|=9\)
\(\Leftrightarrow\orbr{\begin{cases}1-2x=9\\1-2x=-9\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}2x=-8\\2x=10\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=5\end{cases}}\)
\(\left(2x+1\right)\left(y+3\right)=11\)
\(\Rightarrow\left(2x+1\right);\left(y+3\right)\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
Ta có các trường hợp sau :
\(TH1:\hept{\begin{cases}2x+1=1\\y+3=11\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=8\end{cases}}}\) \(TH2:\hept{\begin{cases}2x+1=-1\\y+3=-11\end{cases}\Leftrightarrow\hept{\begin{cases}x=-1\\y=-14\end{cases}}}\)
\(TH3:\hept{\begin{cases}2x+1=11\\y+3=1\end{cases}\Leftrightarrow\hept{\begin{cases}x=5\\y=-2\end{cases}}}\) \(TH4:\hept{\begin{cases}2x+1=-11\\y+3=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-6\\y=-4\end{cases}}\)
Vậy........................................
Đúng 0
Bình luận (0)
Cho x - y = 5 , x^2 + y ^ 2 = 13 . Tính x + y
Ta có: (x-y)^2 = 5^2
x^2 -2xy+ y^2 =25
13 -2xy =25
2xy= -12
xy= -6
Ta có: (x+y)^2 =x^2 +2xy +y^2
= 13+ 2.(-6)
=1
Vậy x+y=1 hoặc x+y= -1
Đúng 0
Bình luận (0)
Tìm các số nguyên x, y sao cho (x - 13).(y + 2) = 13
Tìm x,y e Z tm \(\dfrac{x^2+y^2}{x+y}=\dfrac{85}{13}\)
x+y=5; x^2+y^2=13
tinh x^3+y^3
Ta có: \(x+y=5\)
\(\Rightarrow x^2+2xy+y^2=25\)
\(\Rightarrow2xy=12\)
\(\Rightarrow xy=6\)
Vậy \(x^3+y^3=\left(x+y\right)\left(x^2+y^2+xy\right)\)
\(=5.\left(13+6\right)=95\)
Đúng 0
Bình luận (0)
tính x+y biết x^3+y^3=91 ; x^2 - xy +y^2=13
Tìm các số nguyên x,y sao cho: (x-13).(y+2)=13
Vì \(x,y\inℤ\) và \(\left(x-13\right)\cdot\left(y+2\right)=13\Rightarrow y+2\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
| y+2 | 1 | -1 | 13 | -13 |
x-13 | 13 | -13 | 1 | -1 |
| y | -1 | -3 | 11 | -15 |
| x | 26 | 12 | 14 | -12 |
(x-13).(y+2)=13
=> (y+2)\(\in\)Ư(13)={1;13; -13; -1}
Nếu y+2= 1 => x= 1-2 => y= -1
Nếu y+2=13 => y= 13-2 => y= 11
Nếu y+2= -1 => y= -1-2 => y= -3
Nếu y+2 = -13 => y= -13-2 => y= -15
Sau đó bn thay vào r tự tìm nha
1, Tìm x
a, 2+4+6+....+x= 90
b ( x-1)+(x-2)+....+(x-20)=390
c 1+5+9+13+......+x= 501501
d x.x.+x.2+80
e 4.(x+1)=3.(x+5)
2, tìm x,y
a, x.(y-2)=3
b, x.y+3.x=13
c, (x-1),(y+2)=25
d, x.(y-1)+y=14