Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho MA=ME. Chứng minh AB song song với CE
cho tam giác ABC ,M là trung điểm của BC . Trên tia đối của tia MA lấy điểm E sao cho ME=MA . Chứng minh
a) tam giác ABM= tam giác ECM
b) AB song song CE
Cho tam giác ABC (AB < AC) , AH vuông góc BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HD = HA, gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
a) Chứng minh : AB = CE và BD = CE.
b) Gọi F là trung điểm của DE. Chứng minh MF vuông góc với DE.
c) MF có song song với AD không? Vì sao?
a/ Xét 2 tam giác EMC và tam giác AMB có:
BM=MC (gt)
AM=ME (gt)
Góc AMB=góc EMC (2 góc đối đỉnh)
=> tam giác EMC = tam giác AMB (Cạnh-góc-cạnh)
=> AB=EC (2 cạnh tương ứng)
b/ Xét tam giác ADE có:
AH=HD (gt)
AM=ME (gt)
=> HM là đường trung bình của tam giác ADE => HM//DE => AD vuông góc DE (1)
và DE/2=HM (Tính chất đường trung bình)
Mà DF=FE=DE/2
=> DF=HM=DE/2 (2)
Từ (1) và (2) => Tứ giác HMFD là hình chữ nhật => MF vuông góc DE
c/ MF//DH (cmt)
=> MF//AD
Cho tam giác ABC có M là trung điểm của BC, trên tia đối của MA lấy điểm E sao cho ME = MA. Chứng minh:
a/ tam giác MAB = tam giác MEC
b/ AC song song với BE
c/ Trên AB lấy điểm I, trên CE lấy K sao cho BI = CK. CMR I, M, K thẳng hàng
Cho tam giác ABC có M là trung điểm của BC , trên tia đối của tia MA lấy điểm E sao cho ME = MA . Chứng minh
a, Tam giác MAB = tam giác MEC
b, AC song song với BE
c, Trên tia AB lấy điểm I . Trên cạnh CE lấy điểm K sao cho BI = CKK . Chứng minh I,M,K thẳng hàng
trình bày cách làm nữa nha
Xét ABM và EMC có : AM = ME BM = CM Góc AMB = góc CME ( đối đỉnh ) => tam giac ABM = Tam giác EMC Ta có : Tam giác AMB = tam giác EMC nên góc BAM = góc EMC Mặt khác : 2 góc BAM và AEC nắm vị trí so le trong => AB // CE c Xét tam giác AIB và tam gics CIK có : AI = IC BI = Ik Góc AIB = góc CIK ( đối đỉnh ) => tam giác AIB = tam giác CIK
Cho tam giác ABC có M là trung điểm của BC , trên tia đối của tia MA lấy điểm E sao cho ME = MA . Chứng minh
a, Tam giác MAB = tam giác MEC
b, AC song song với BE
c, Trên tia AB lấy điểm I . Trên cạnh CE lấy điểm K sao cho BI = CKK . Chứng minh I,M,K thẳng hàng
trình bày cách làm nữa nha
Xét ABM và EMC có :
AM = ME
BM = CM
Góc AMB = góc CME ( đối đỉnh )
=> tam giac ABM = Tam giác EMC
Ta có : Tam giác AMB = tam giác EMC nên góc BAM = góc EMC
Mặt khác : 2 góc BAM và AEC nắm vị trí so le trong
=> AB // CE
c Xét tam giác AIB và tam gics CIK có :
AI = IC
BI = Ik
Góc AIB = góc CIK ( đối đỉnh )
=> tam giác AIB = tam giác CIK
Sửa đề: ΔABC vuông tại A
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
vậy: BC=10cm
b) Xét ΔAMC và ΔEMB có
CM=BM(M là trung điểm của BC)
\(\widehat{AMC}=\widehat{BME}\)(hai góc đối đỉnh)
MA=ME(gt)
Do đó: ΔAMC=ΔEMB(c-g-c)
Suy ra: AC=BE(hai cạnh tương ứng)
Xét ΔAMB và ΔEMC có
AM=EM(gt)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔEMC(c-g-c)
Suy ra: \(\widehat{BAM}=\widehat{CEM}\)(hai góc tương ứng)
mà \(\widehat{BAM}\) và \(\widehat{CEM}\) là hai góc ở vị trí so le trong
nên AB//EC(Dấu hiệu nhận biết hai đường thẳng song song)
cho tam giác ABC có góc B = 90 độ , vẽ trung tuyến AM . trên tia đối của tia MA lấy điểm E sao cho ME=MA .chứng minh
a) tam giác ABM= tam giác ECM
b) BE song song với AC
c)gọi N là trung điểm của CE . BN cắt CE tại G. biết AB=30cm,BC=4cm. tính BG
a: Xét ΔMBA và ΔMCE có
MB=MC
góc BMA=góc CME
MA=ME
=>ΔMBA=ΔMCE
b: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
=>ABEC là hình bình hành
=>BE//AC
cho tam giác ABC , M là trung điểm của BC . trên tia đối của tia MA lấy điểm E sao cho ME=MA . chứng minh AB//CE
Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
a) Chứng minh:
b) Chứng minh: AB //CE
Hình vẽ mình họa
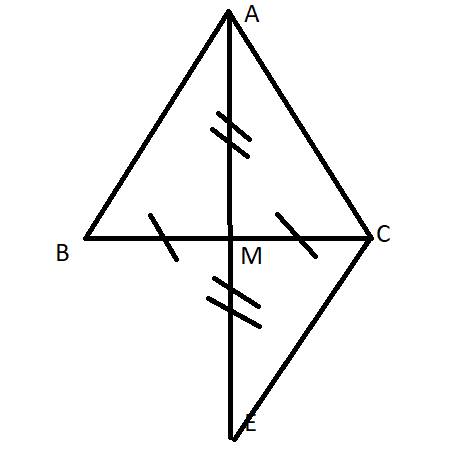
a, CM j cậu nhỉ .-.?
b, +)Xét ΔBAM và ΔCEM
AM=ME(GT)
BM=CM(M là trung điểm của BC)
\(\widehat{BMA}=\widehat{CME}\)(đối đỉnh)
=>ΔBAM=ΔCEM(c.g.c)
=>\(\widehat{BAE}=\widehat{AEC}\) (cạnh tương ứng)
+)\(\widehat{BAE}=\widehat{AEC}\) mà 2 góc này nằm ở vị trí so le trong
=>AB//CE