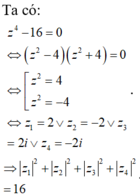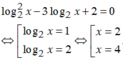Tính tổng bình phương tất cả các nghiệm của phương trình:

Những câu hỏi liên quan
Trên tập số phức, tính tổng môđun bình phương tất cả các nghiệm của phương trình
z
4
-
16
0
Đọc tiếp
Trên tập số phức, tính tổng môđun bình phương tất cả các nghiệm của phương trình z 4 - 16 = 0
![]()
![]()
![]()
![]()
Trên tập số phức, tính tổng môđun bình phương tất cả các nghiệm của phương trình
z
4
-
16
0
.
Đọc tiếp
Trên tập số phức, tính tổng môđun bình phương tất cả các nghiệm của phương trình z 4 - 16 = 0 .
![]()
![]()
![]()
![]()
Tổng bình phương tất cả các nghiệm của phương trình
log
2
2
x
-
3
log
3
x
.
log
2
3
+
2
0
bằng A. 25. B. 20. C. 18. D. 6.
Đọc tiếp
Tổng bình phương tất cả các nghiệm của phương trình log 2 2 x - 3 log 3 x . log 2 3 + 2 = 0 bằng
A. 25.
B. 20.
C. 18.
D. 6.
Đặt T là tổng bình phương tất cả các nghiệm của phương trình
1
6
−
log
2
4
x
+
2
2
+
log
2
x
1.
Vậy T bằng A. 6 B. 20 C. 36 D. 2
Đọc tiếp
Đặt T là tổng bình phương tất cả các nghiệm của phương trình
1
6
−
log
2
4
x
+
2
2
+
log
2
x
=
1.
Vậy T bằng
A. 6
B. 20
C. 36
D. 2
Đáp án B
Điều kiện:
x > 0 log 2 4 x ≠ 6 log 2 x ≠ − 2 ⇔ x > 0 x ≠ 16 x ≠ 1 4 .
1 6 − log 2 4 x + 2 2 + log 2 x = 1 ⇔ 1 4 − log 2 x + 2 2 + log 2 x = 1 ⇔ 2 + log 2 x + 8 − 2 log 2 x 4 − log 2 x 2 + log 2 x = 1 ⇔ 10 − log 2 x = − log 2 2 x + 2 log 2 x + 8 ⇔ − log 2 2 x + 3 log 2 x − 2 = 0 ⇔ log 2 x = 1 log 2 x = 2 ⇔ x = 2 x = 4 .
Vậy tổng bình phương tất cả các nghiệm của phương trình bằng 20
Đúng 0
Bình luận (0)
Câu 1: Tính tổng tất cả các nghiệm của phương trình sin3(x-dfrac{pi}{4}) sqrt{2}sinx trên đoạn [0 ; 2018]Câu 2: Tính tổng tất cả các nghiệm của phương trình cos2x (tan2x - cos2x) cos3x - cos2x + 1 trên đoạn [0 ; 43π]GIÚP MÌNH VỚI!!!
Đọc tiếp
Câu 1: Tính tổng tất cả các nghiệm của phương trình sin3(\(x-\dfrac{\pi}{4}\)) = \(\sqrt{2}\)sinx trên đoạn [0 ; 2018]
Câu 2: Tính tổng tất cả các nghiệm của phương trình cos2x (tan2x - cos2x) = cos3x - cos2x + 1 trên đoạn [0 ; 43π]
GIÚP MÌNH VỚI!!!![]()
Cho phương trình
2
-
m
3
-
3
m
2
+
1
.
log
81
x...
Đọc tiếp
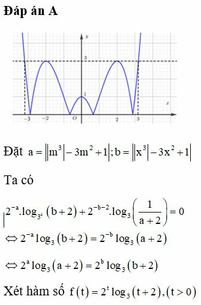
Cho phương trình 2 - m 3 - 3 m 2 + 1 . log 81 x 3 - 3 x 2 + 1 + 2 + 2 - x 3 - 3 x 2 + 1 - 2 . log 3 1 m 3 - 3 m 2 + 1 + 2 = 0 . Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có số nghiệm thuộc đoạn 6 ; 8 . Tính tổng bình phương tất cả các phần tử của tập S.
A. 20
B. 28
C. 14
D. 10
Cho phương trình
2
cos
2
x
cos
2
x
−
cos
2018
π
2
x
cos
4
x
−
1
. Tính tổng tất cả các nghiệm thực dương của phương trình. A.
π
B....
Đọc tiếp
Cho phương trình 2 cos 2 x cos 2 x − cos 2018 π 2 x = cos 4 x − 1 . Tính tổng tất cả các nghiệm thực dương của phương trình.
A. π
B. 1010 π
C. 1001 π
D. 1100 π
Đáp án B.
Điều kiện: x ≠ 0 .
Ta có 2 cos 2 x cos 2 x − cos 2018 π 2 x = cos 4 x − 1
⇔ 2 cos 2 2 x − 2 cos 2 x . cos 2018 π 2 x = cos 4 x − 1
⇔ cos 4 x + 1 − 2 cos 2 x . cos 2018 π 2 x = cos 4 x − 1
⇔ cos 2 x . cos 2018 π 2 x = 1
ta có cos 2 x . cos 2018 π 2 x ≤ 1
do đó cos 2 x . cos 2018 π 2 x = 1 ⇔ cos 2 x = 1 cos 2018 π 2 x = 1 hoặc cos 2 x = − 1 cos 2018 π 2 x = − 1
cos 2 x = 1 cos 2018 π 2 x = 1 ⇔ x = k π x = 1009 π l k , l ∈ ℤ
⇒ k l = 1009 ⇒ k = 1009 l = 1 hoặc k = − 1009 l = − 1 hoặc k = 1 l = 1009 hoặc k = − 1 l = − 1009
Trong trường hợp này tổng các nghiệm dương của phương trình bằng 1010 π
cos 2 x = − 1 cos 2018 π 2 x = − 1 ⇔ x = π 2 + k π x = 2018 π 1 + 2 l k , l ∈ ℤ
⇒ 1 2 + k = 2018 1 + 2 l ⇒ 1 + 2 k 1 + 2 l = 2.2018 (*)
Vế trái của (*) là số lẻ, vế phải của (*) là số chẵn. Do đó không có giá trị nguyên nào của k, l thỏa mãn (*).
* Tóm lại: Tổng các nghiệm dương của phương trình bằng 1010π.
Đúng 0
Bình luận (0)
Tính tổng bình phương tất cả các nghiệm của phương trình:
\(\left(2x+1\right)\left(x+1\right)^2\left(2x+3\right)=18\)
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
A. -1
B. -2
C. -3
D. -4
Chọn D.
Phương trình đã cho tương đương với phương trình
z( z + 2) ( z - 1) ( z + 3)
Hay ( z2 + 2z) ( z2 + 2z - 3) = 10
Đặt t = z2 + 2z. Khi đó phương trình trở thành: t2 - 2t – 10 = 0.
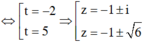
Vậy phương trình có các nghiệm: ![]()
Tổng tất cả các phần thực của các nghiệm phương trình đã cho là:
-1+ ( -1) + (-1) + ( -1) = -4.
Đúng 0
Bình luận (0)
Tổng bình phương tất cả các nghiệm của phương trình: (2x + 1)(x + 1)2(2x + 3) = 18 là bao nhiêu
ta có (2x+1)(x-1)2(2x+3)=(4x2+8x+3)(x2+2x+1)=18
đặt x2+2x+1=a ta có (4a-1)a=18
giải hệ trên ta được 2 nghiệm x=0,5 và x=-2,5
đến đay các ban tự giai tiếp nhé
Đúng 0
Bình luận (0)