Cho tam giác ABC, đường phân giác của A cắt BC tại D. Chứng minh DB/DC=AB/AC

Những câu hỏi liên quan
Cho tam giác ABC với AB > AC. Tia phân giác của góc A cắt BC tại D. Chứng minh: DB - DC < AB - AC
cho tam giác ABC vuông tại A, AB=12cm; AC=16cm. Vẽ đường cao AH (H thuộc BC). Đường phân giác BD của góc ABC cắt AH tại E ( D thuộc AC)
a) Chứng minh: AB^2 = BH.BC
b) Tính AD
C) Chứng minh: DB/EB = DC/DA
a: ΔACB vuông tại A co AH vuông góc BC
nên AB^2=BH*BC
b: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=16/8=2
=>AD=6cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB > AC. Tia phân giác của góc A cắt BC tại D. Chứng minh : DB - DC < AB - AC
CHO TAM GIÁC ABC VỚI AB>AC, TIA PHÂN GIÁC CỦA GÓC A CẮT BC TẠI D. Chứng minh DB-DC<AB-AC
90=12340-12357680-3568990-35667888
24678017890-6543456789
1`234567890-=34567890-
234567890-=234567890
34567890-4567890
3456745678
4567890-567890-=
45678904567890-
45678890455678990
4567890-4567890-
5678904567890-67890-
Đúng 0
Bình luận (0)
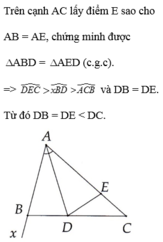
Cho tam giác ABC có AB < AC. Tia phân giác góc A cắt cạnh BC tại D. Chứng minh DB < DC.
cho tam giác ABC có B = C . Tia phân giác của góc A cắt BC tại D chứng minh DB = DC, AB = AC
Tam giác ABC có góc B = góc C
=> ABC là tam giác cân (hai góc kề cạnh đáy bằng nhau)
=> AB = AC
Xét hai tam giác BAD và CAD có:
AC = AB (cmt)
góc BAD = góc CAD (AD là phân giác của góc A)
góc B = góc C (gt)
=> tam giác BAD = tam giác CAD (g.c.g)
=> DB = DC
Đúng 1
Bình luận (0)
*Vì tam giác ABC co góc B=C
=>tam giác ABC là tam giác cân
=>AB=AC
* Xét hai tam giác ABD và tam giác ADC có:
AB=AC(chứng minh trên)
góc B=góc C(GIẢ THIẾT)
AD là cạnh chung
=>tam giác ABD=ADC(c-g-c)
=>DB=DC(2 cạnh tương ứng)
Đúng 0
Bình luận (0)
Xét tam giác ABC , ta có :
\(\widehat{B}\)= \(\widehat{C}\) (giả thuyết)
=> Tam giác ABC cân tại \(\widehat{A}\)
=> AB = AC (tính chất tam giác cân)
Vì tam giác ABC cân tại \(\widehat{A}\)
=> AD là đường phân giác
=> DB = DC
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có AB<AC. Tia phân giác của góc A cắt BC tại D. Chứng minh DB<DC
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Qua C kẻ đường thẳng song song với AB cắt AD tại E.
a) Chứng minh: ∆ABD ∽ ∆ECD
b) Cho AB = 8cm, AC = 12cm, BC =15cm. Tính DB, DC.
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Qua C kẻ đường thẳng song song với AB cắt AD tại E.
a) Chứng minh: ∆ABD ∽ ∆ECD
b) Cho AB = 8cm, AC = 12cm, BC =15cm. Tính DB, DC.
a: Xét ΔABD và ΔECD có
\(\widehat{ADB}=\widehat{EDC}\)
\(\widehat{ABD}=\widehat{ECD}\)
Do đó; ΔABD\(\sim\)ΔECD
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{2}=\dfrac{DC}{3}=\dfrac{DB+DC}{2+3}=\dfrac{15}{5}=3\)
Do đó: DB=6cm; DC=9cm
Đúng 1
Bình luận (0)