\(x^2+y^2=325\)

<=>  \(\left(x+y\right)^2-2xy=325\)

Đặt:  \(x+y=a;\)\(xy=b\)Khi đó ta có:

\(a-b=155\)   (1)

và  \(a^2-2b=325\)

Từ (1) ta có:   \(b=a-155\) thay vào (2) ta được:

\(a^2-2\left(a-155\right)=325\)

giải ra tìm được:  \(\orbr{\begin{cases}a=5\\a=-3\end{cases}}\)  =>  \(\orbr{\begin{cases}a=5;b=-150\\a=-3;b=-158\end{cases}}\)

TH1:  \(\hept{\begin{cases}a=5\\b=-150\end{cases}}\) ,=>  \(\hept{\begin{cases}x+y=5\\xy=-150\end{cases}}\)

\(x^2+y^2=325\) 

<=>   \(\left(x-y\right)^2+2xy=325\)

<=>  \(\left(x-y\right)^2=325-2xy=625\)

<=>  \(\left|x-y\right|=25\)

=>  \(\left|x^3-y^3\right|=\left|\left(x-y\right)\left(x^2+y^2+xy\right)\right|=\left|x-y\right|\left(x^2+y^2+xy\right)=4375\)

TH2: bn tự lm tiếp nhé

quên mất rồi!

Lê Đức Huy sai rồi bạn phải là x²-y-y²-x=0 chứ bạn

Lê Nhật Minh này! Bạn k bt thì đừng nói. Có phải bài nào cx giống nhau đâu, mak có thế thì bạn cx sai

\(A=\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)+\left(\dfrac{1}{2xy}+8xy\right)+\dfrac{3}{xy}\)

\(A\ge\dfrac{4}{x^2+y^2+2xy}+2\sqrt{\dfrac{8xy}{2xy}}+\dfrac{3}{\dfrac{1}{4}\left(x+y\right)^2}\ge20\)

\(A_{min}=20\) khi \(x=y=\dfrac{1}{2}\)

\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\frac{x-1+y-2+z-3}{2+3+4}=\frac{2x-2+3y-6-z+3}{4+9-4}=\frac{45}{9}=5\)

=>\(\frac{x+y+z-6}{9}=5\Rightarrow x+y+z=45+6=51\)

cái thằng lê duy minh ăn hại thì có,5**** 100 phần trăm.

Đáp án D.

Ta có

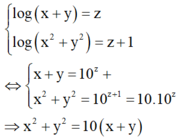
Khi đó

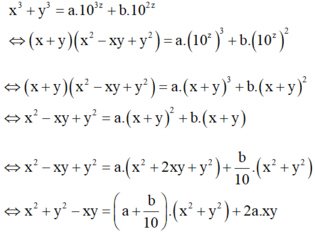
Đồng nhất hệ số, ta được