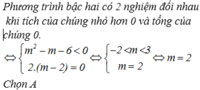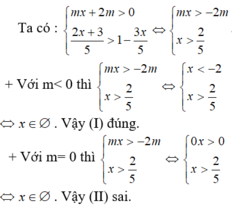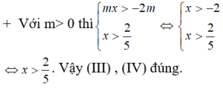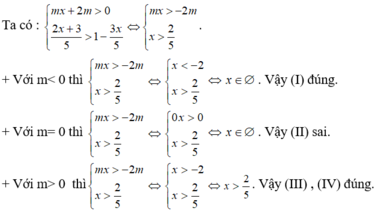Phương trình \(m^2x+2=x+2m\) có tập nghiệm S=R khi và chỉ khi

Những câu hỏi liên quan
(Em cần lời giải chi tiết ạ! Cảm ơn mọi người)
Câu 1: Tập hợp các giá trị thực của tham số m để phương trình sqrt{x^2+2x+2m}2x+1 có hai nghiệm phân biệt là S (a;b]. Khi đó P a.b là....
Câu 2: Cho phương trình sqrt{-x^2+4x-3}sqrt{2m+3x-x^2}. Để phương trình có nghiệm thì m ϵ [a;b]. Giá trị a^2+b^2?
Câu 3: Biết phương trình x^4-3mx^2+m^2+10 có 4 nghiệm phân biệt x_1,x_2,x_3,x_4. Tính M x1+x2+x3+x4+x1x2x3x4
Đọc tiếp
(Em cần lời giải chi tiết ạ! Cảm ơn mọi người)
Câu 1: Tập hợp các giá trị thực của tham số m để phương trình \(\sqrt{x^2+2x+2m}=2x+1\) có hai nghiệm phân biệt là S = (a;b]. Khi đó P = a.b là....
Câu 2: Cho phương trình \(\sqrt{-x^2+4x-3}=\sqrt{2m+3x-x^2}\). Để phương trình có nghiệm thì m ϵ [a;b]. Giá trị \(a^2+b^2=?\)
Câu 3: Biết phương trình \(x^4-3mx^2+m^2+1=0\) có 4 nghiệm phân biệt \(x_1,x_2,x_3,x_4\). Tính M = x1+x2+x3+x4+x1x2x3x4
1.
\(2x+1\ge0\Rightarrow x\ge-\dfrac{1}{2}\)
Khi đó pt đã cho tương đương:
\(x^2+2x+2m=\left(2x+1\right)^2\)
\(\Leftrightarrow x^2+2x+2m=4x^2+4x+1\)
\(\Leftrightarrow3x^2+2x+1=2m\)
Xét hàm \(f\left(x\right)=3x^2+2x+1\) trên \([-\dfrac{1}{2};+\infty)\)
\(-\dfrac{b}{2a}=-\dfrac{1}{3}< -\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{2}\right)=\dfrac{3}{4}\) ; \(f\left(\dfrac{1}{3}\right)=\dfrac{2}{3}\)
\(\Rightarrow\) Pt đã cho có 2 nghiệm pb khi và chỉ khi \(\dfrac{2}{3}< 2m\le\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{1}{3}< m\le\dfrac{3}{8}\)
\(\Rightarrow P=\dfrac{1}{8}\)
Đúng 1
Bình luận (0)
3.
Đặt \(x^2=t\ge0\Rightarrow\left[{}\begin{matrix}x=\sqrt{t}\\x=-\sqrt{t}\end{matrix}\right.\)
Pt trở thành: \(t^2-3mt+m^2+1=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương pb
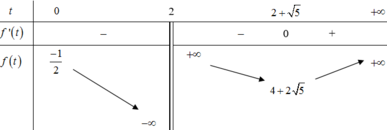
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=9m^2-4\left(m^2+1\right)>0\\t_1+t_2=3m>0\\t_1t_2=m^2+1>0\end{matrix}\right.\) \(\Rightarrow m>\dfrac{2}{\sqrt{5}}\)
Ta có:
\(M=x_1+x_2+x_3+x_4+x_1x_2x_3x_4\)
\(=-\sqrt{t_1}-\sqrt{t_2}+\sqrt{t_1}+\sqrt{t_2}+\left(-\sqrt{t_1}\right)\left(-\sqrt{t_2}\right)\sqrt{t_1}.\sqrt{t_2}\)
\(=t_1t_2=m^2+1\) với \(m>\dfrac{2}{\sqrt{5}}\)
Đúng 1
Bình luận (0)
2.
ĐKXĐ: \(1\le x\le3\)
Pt tương đương:
\(-x^2+4x-3=2m+3x-x^2\)
\(\Leftrightarrow x=2m+3\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(1\le2m+3\le3\)
\(\Leftrightarrow-1\le m\le0\)
\(\Rightarrow a^2+b^2=1\)
Đúng 1
Bình luận (0)
Phương trình
x
2
-
2
m
-
2
x
+
m
2
-
m
-
6
0
có hai nghiệm đối nhau khi và chỉ khi A.
m
2
B. -3m2 C.
m
-
2
hoặc
m
3
D. -2m3
Đọc tiếp
Phương trình x 2 - 2 m - 2 x + m 2 - m - 6 = 0 có hai nghiệm đối nhau khi và chỉ khi
A. m = 2
B. -3<m<2
C. m < - 2 hoặc m > 3
D. -2<m<3
Bất phương trình mx^2−2(m−1)x+4m >0 có tập nghiệm là R khi và chỉ khi nào?
Online chờ gấp, đa ta các vị!
TH1: `m=0 `
`2x>0 <=> x>0`
`=>` Không thỏa mãn.
TH2: `m>0`
Bất PT có tập nghiệm là `RR <=> \Delta'<0`
`<=> (m-1)^2-m.4m<0`
`<=> m<-1 ; 1/3 <m`
Vậy `m in (0;+∞)` thỏa mãn.
Đúng 0
Bình luận (3)
Phương trình x 2 - 2 m + 2 x + m 2 - m - 6 = 0 luôn có hai nghiệm trái dấu khi và chỉ khi
A. m<-2
B. -3<m<2
C. -2
D. -2<m<3
Để phương trình đã cho có hai nghiệm trái dấu khi:
a c = m 2 - m - 6 < 0 ⇔ - 2 < m < 3
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho hệ bất phương trình
mx
+
2
m
0
2
x
+
3
5...
Đọc tiếp
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R
(III) Khi m≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là 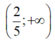
(IV) Khi m> 0 thì hệ bất phương trình đã cho có tập nghiệm là 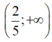
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
Cho hệ bất phương trình
mx
+
2
m
0
2
x
+
3
5...
Đọc tiếp
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R.
(III) Khi m ≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
(IV) Khi m > 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
Gọi S là tập hợp các giá trị thực của tham số m để phương trình
4
x
-
m
.
2
x
+
2
m
+
1
0
có nghiệm. Tập RS có bao nhiêu giá trị nguyên? A.1 B.4 C.9 D.7
Đọc tiếp
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x - m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên?
A.1
B.4
C.9
D.7
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x – m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên
A. 1
B. 4
C. 9
D. 7
Cho phương trình
m
2
+
m
−
6
x
2
m
−
2
m
−
3
trong đó m là tham số.a) Chứng minh:i) Khi m 2 phương trình có tập nghiệm là
ℝ
; ii) Khi m -3 phương trìn...
Đọc tiếp
Cho phương trình m 2 + m − 6 x 2 = m − 2 m − 3 trong đó m là tham số.
a) Chứng minh:
i) Khi m = 2 phương trình có tập nghiệm là ℝ ;
ii) Khi m = -3 phương trình có tập nghiệm là ∅ .
b) Giải phương trình đã cho khi m = 5.