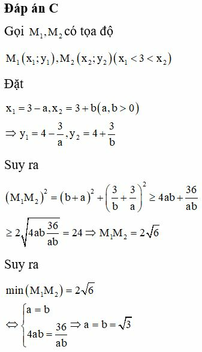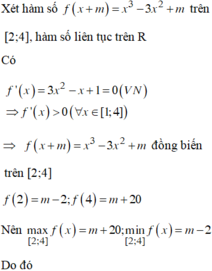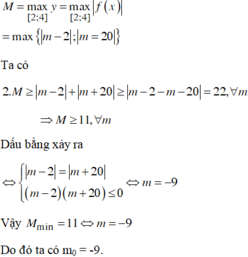Tìm giá trị của x để -3x2+9x-22015 đạt giá trị nhỏ nhất ..giúp mik vs nha .

Những câu hỏi liên quan
Tìm x để A đạt giá trị nhỏ nhất, tìm giá trị nhỏ nhất:
A = |x-5| + |x+3|
Ai làm nhanh và đúng mik tick cho nha :))
\(A=\left|x-5\right|+\left|x+3\right|\ge\left|5-x+x+3\right|=8\)
Dấu " = " xảy ra <=> \(\hept{\begin{cases}x-5\ge0\\x+3\ge0\end{cases}\Rightarrow\hept{\begin{cases}x\ge5\\x\ge-3\end{cases}\Rightarrow}x\ge5}\)
Vậy,..........
Đúng 0
Bình luận (0)
giá trị của x để giá trị biểu thức -3x^2+9x-2^2015 đạt giá trị nhỏ nhất
giá trị nhỏ nhất của x để : (9x^2-48x+65) đạt giá trị nhỏ nhất
Lời giải:
$9x^2-48x+65=(3x)^2-2.3x.8+8^2+1=(3x-8)^2+1\geq 0+1=1$
Vậy $9x^2-48x+65$ nhận giá trị nhỏ nhất bằng $1$.
Giá trị này đạt tại $3x-8=0\Leftrightarrow x=\frac{8}{3}$
Đúng 0
Bình luận (0)
cho phân thức C=3x^2-x/9x^2-6x+1
d/ tìm x để giá trị của phân thức nhận giá trị âm
giải kỹ vs nhanh hộ mik vs nha mai mik kt r!!!cảm ơn trc nhaaa![]()
Câu hỏi khống chế điểm 10 của trường mk nè:
Tìm giá trị của x và y để: S = (x + 2)4 + |2y - 10| + 2017 đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó
Giải chi tiết giúp mk nha!!!Có tick cho người nhanh nhất ^_-
Ta có: (x + 2)4 \(\ge\)0 với mọi x
|2y - 10| \(\ge\)0 với mọi y
=> (x + 2)4 + |2y - 10| \(\ge\)0
=> S = (x + 2)4 + |2y - 10| + 2017 \(\ge\)2017
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left(x+2\right)^4=0\\\left|2y-10\right|=0\end{cases}}\)<=>\(\hept{\begin{cases}x=-2\\y=5\end{cases}}\)
Vậy GTNN của S = 2017 tại x = -2 và y = 5
Đúng 0
Bình luận (0)
Tìm trên mỗi nhánh của đồ thị
C
:
y
4
x
-
9
x
-
3
các điểm
M
1
,
M
2
để độ dài
M
1
M
2
đạt giá trị nhỏ nhất, giá trị nhỏ nhất đó...
Đọc tiếp
Tìm trên mỗi nhánh của đồ thị C : y = 4 x - 9 x - 3 các điểm M 1 , M 2 để độ dài M 1 M 2 đạt giá trị nhỏ nhất, giá trị nhỏ nhất đó bằng
A. 2 5
B. 2 2
C. 2 6
D. 3 2
Biết rằng hàm số
f
(
x
)
x
3
-
3
x
2
-
9
x
+
28
đạt giá trị nhỏ nhất trên đoạn [0;4] tại
x
0
.Tính
P
x
0
+
2018
A. P 2021 B. P 2018 C. P 2019 D. P 3
Đọc tiếp
Biết rằng hàm số f ( x ) = x 3 - 3 x 2 - 9 x + 28 đạt giá trị nhỏ nhất trên đoạn [0;4] tại x 0 .Tính P = x 0 + 2018
A. P = 2021
B. P = 2018
C. P = 2019
D. P = 3
Gọi M là giá trị lớn nhất của hàm số
y
x
3
-
3
x
2
+
x
+
m
xét trên đoạn [2;4],
m
0
là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng. A.
1...
Đọc tiếp
Gọi M là giá trị lớn nhất của hàm số y = x 3 - 3 x 2 + x + m xét trên đoạn [2;4], m 0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
A. 1 < m 0 < 5
B. - 7 < m 0 < - 5
C. - 4 < m 0 < 0
D. m 0 < - 8
Gọi M là giá trị lớn nhất của hàm số y
x
3
-
3
x
2
+
x
+
m
xét trên đoạn [2;4], m0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng. A. 1
m
0
5 B. -7
m...
Đọc tiếp
Gọi M là giá trị lớn nhất của hàm số y = x 3 - 3 x 2 + x + m xét trên đoạn [2;4], m0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
A. 1 < m 0 < 5
B. -7 < m 0 < -5
C. -4 < m 0 < 0
D. m 0 < -8
Chọn D.
Xét hàm số ![]() hàm số liên tục trên R
hàm số liên tục trên R
Có ![]()
![]()
![]() đồng biến trên [2;4]
đồng biến trên [2;4]
![]()
Nên ![]()
Do đó ![]()
![]()
Ta có ![]()
![]()
![]()
Dấu bằng xảy ra 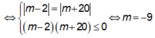
Vậy ![]()
![]()
Đúng 0
Bình luận (0)