dm vuông là gì

Những câu hỏi liên quan
cho tam giác ABC. Vẽ phía ngoài tam giác các tam giác vuông tại A là ABD và ACE có AB=AD, AC=AE. Kẻ AH vuông góc với BC, DM vuông góc với AH,EN vuông goc với AH.Chứng minh rằng
a, DM=AH, EN=AH
b, có nhận xét gì DM và EN
c, Gọi O là giao điểm của AN và DE.chứng minh O là trung điểm của DE
Cho tam giác ABC vuông tại A. D là trung điểm BC.Từ D kẻ DM vuông góc AB tại M,DN vuông góc AC tại N
a)tứ giác AMDN là hình gì?VÌ sao?
b)Gọi K là điểm đối xứng với D qua N.Tứ giác ADCK là hình gì?Vì sao?
c) để tứ giác ADCK là hình vuông thì tam giác ABC thêm điều kiện gì?
Câu 1: Cho tam giác DEF vuông tại D có DE = 12cm, DF = 9cm, DM là đường trung tuyến (M thuộc EF). a) Tính EF, DM. b) Gọi N và K lần lượt là chân các đường vuông góc hạ từ M xuống DE và DF. Tứ giác DNMK là hình gì? Vì sao? c) Gọi H là điểm đối xứng với M qua N, O là trung điểm của MD. Chứng minh rằng ba điểm H, O, F thẳng hàng rồi.
a: ΔDEF vuông tại D
=>\(DE^2+DF^2+EF^2\)
=>\(EF^2=9^2+12^2=225\)
=>\(EF=\sqrt{225}=15\left(cm\right)\)
Ta có; ΔDEF vuông tại D
mà DM là đường trung tuyến
nên \(DM=\dfrac{EF}{2}=7,5\left(cm\right)\)
b: Xét tứ giác DNMK có
\(\widehat{DNM}=\widehat{DKM}=\widehat{KDN}=90^0\)
=>DNMK là hình chữ nhật
c: Xét ΔDEF có MN//DF
nên \(\dfrac{MN}{DF}=\dfrac{EM}{EF}\)
=>\(\dfrac{MN}{DF}=\dfrac{1}{2}\)
mà \(MN=\dfrac{1}{2}MH\)
nên MH=DF
Ta có: MN//DF
N\(\in\)MH
Do đó: MH//DF
Xét tứ giác DHMF có
MH//DF
MH=DF
Do đó: DHMF là hình bình hành
=>DM cắt HF tại trung điểm của mỗi đường
mà O là trung điểm của DM
nên O là trung điểm của HF
=>H,O,F thẳng hàng
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có góc A vuông, D là trung điểm của BC, từ D kẻ DM vuông góc với AB tại M, DN vuông góc với AC tại N.
a) Tứ giác AMDN là hình gì? Vì sao?
b) Gọi K là điểm đối xứng với D qua N. Tứ giác ADCK là hình gì? Vì sao?
Giúp mình với ạ:<
Cho hình thang vuông ABCD có góc A = góc D = 90, AB = AD = ½ CD. Gọi E là trung điểm của CD
a) Tứ giác ABCE là hình gì vì sao
b) Tứ giác ABED là hình gì vì sao
c) Gọi M là giao điểm của AC va BE, K là gia điểm của AE và DM. Kẻ DH vuông góc với AC cắt AE ở I. chứng minh BIDK là hình thoi
giúp mk vs ạ
Cho tam giác DEF vuông tại D, đường trung tuyến DM. Gọi K là trung điểm của ED, A là điểm đối xứng với M qua K
a) Chứng minh điểm A đối xứng với điểm M qua DE
b) Tứ giác là hình gì? Vì sao?
c) Tam giác DEF có điều kiện gì thì DAEM là hình vuông
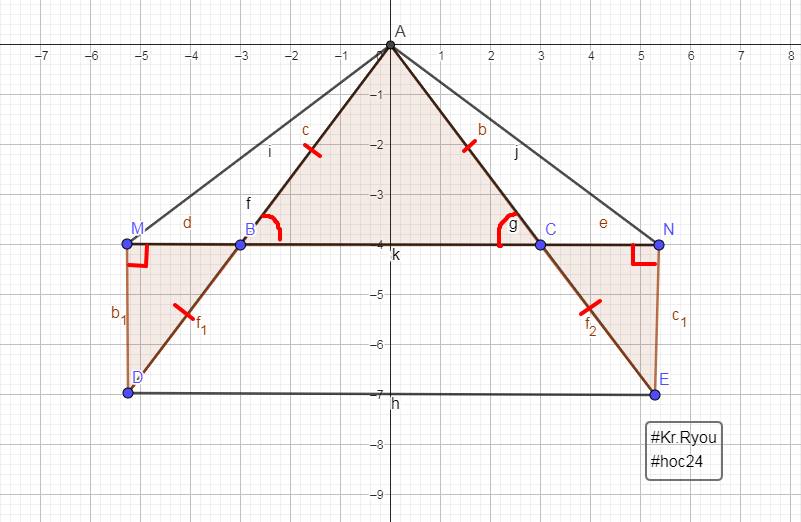
Cho▲ABC cân tại A, trên tia đối của tia của tia BA và CA lấy D và E sao cho BD=CE.c/m:
a)DE song song với BC
b)kẻ DM vuông góc với BC, EN vuông góc với BC, c/m DM=EN
c)▲AMN là ▲ gì?
VẼ HÌNH GIÚP!
`#040911`
a)
Ta có:
\(\left\{{}\begin{matrix}\text{AB = AC (tg ABC cân tại A)}\\\text{BD = CE (gt)}\end{matrix}\right.\)
`\Rightarrow \text {AD = AE}`
Xét `\Delta ADE:`
`AD = AE`
`\Rightarrow Delta ADE` cân tại A
`\Rightarrow`\(\widehat{\text{ADE}}=\widehat{\text{AED}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(1)`
`\Delta ABC` cân tại A
`\Rightarrow`\(\widehat{\text{ABC}}=\widehat{\text{ACB}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(2)`
Từ `(1)` và `(2)`
`\Rightarrow`\(\widehat{\text{ABC}}=\widehat{\text{ADE}}\)
Mà `2` góc này nằm ở vị trí đồng vị
`\Rightarrow \text {DE // BC (t/c 2 dt' //)}`
b)
Ta có:
\(\widehat{ABC}=\widehat{ACB}\text{ }\left(\Delta ABC\text{ cân tại A}\right)\)
Mà \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{MBD}\text{ }\left(\text{đối đỉnh}\right)\\\widehat{ACB}=\widehat{NCE}\text{ }\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
`\Rightarrow`\(\widehat{\text{MBD}}=\widehat{\text{NCE}}\)
Xét `\Delta MBD` và `\Delta NCE:`
\(\widehat{\text{BMD}}=\widehat{\text{CNE}}\left(=90^0\right)\)
\(\text{BD = CE (gt)}\)
\(\widehat{\text{MBD}}=\widehat{\text{NCE}}\text{ (CMT)}\)
`\Rightarrow Delta MBD = \Delta NCE (ch - gn)`
`\Rightarrow \text {DM = EN (2 cạnh tương ứng)}`
c)
Vì `\Delta MBD = \Delta NCE (b)`
`\Rightarrow \text {BM = CN (2 cạnh tương ứng)}`
Ta có:
\(\left\{{}\begin{matrix}\widehat{\text{ABM}}+\widehat{\text{ABC}}=180^0\text{ (kề bù)}\\\widehat{\text{ACN}}+\widehat{\text{ACB}}=180^0\text{ (kề bù)}\end{matrix}\right.\)
Mà \(\widehat{\text{ABC}}=\widehat{\text{ACB}}\) `(\Delta ABC` cân tại A`)`
`\Rightarrow`\(\widehat{\text{ABM}}=\widehat{\text{ACN}}\)
Xét `\Delta AMB` và `\Delta ANC:`
\( \text{AB = AC }\left(\Delta\text{ABC cân tại A}\right)\\ \widehat{\text{ABM}}=\widehat{\text{ACN}}\\ \text{BM = CN (CMT)}\)
`\Rightarrow \Delta AMB = \Delta ANC (c-g-c)`
`\Rightarrow \text {AM = AN (2 cạnh tương ứng)}`
Xét `\Delta AMN`
`\text {AM = AN}`
`\Rightarrow \Delta AMN` là `\Delta` cân.
Đúng 3
Bình luận (0)
bn ơi mình thấy câu b kẻ thêm nó cứ sao ý
bn có chép đúng đề bài ko
Xem thêm câu trả lời
cho tam giác ABC vẽ phía ngoài tam giác ABC các tam giác tại A là ABD , ACE có AB= AD , AC=AE
Kẻ AH vuông góc với BC , DM vuông góc với AH , EN vuông góc với AH
a) DAM=ABH và DM = AH
b) EN = AH có nhận xét gì về DM và EN
b) Gọi O là giao điểm của AN và De
chứng minh rằng O là trung điểm của DE
Bài 1 : Cho tam giác ABC vuông tại A , trung tuyến AD (D thuộc BC) .Kẻ DM vuông góc với AB . DN vuông góc với AC (M thuộc AB , N thuộc AC) a, Tứ giác ANDM là hình gì ? Vì sao ? b, E đối xứng với D qua M . CMR :AE //MN c, Tứ giác ADBE là hình gì ? Vì sao? . Nhớ kẻ hình nhé
Xem chi tiết
a: Xét tứ giác ANDM có
\(\widehat{AND}=\widehat{AMD}=\widehat{MAN}=90^0\)
Do đó: ANDM là hình chữ nhật
Đúng 2
Bình luận (0)



















