cho x là số thực thỏa mãn x2-4x+1=0.tính giá trị biểu thức A=x5+1/x5

Những câu hỏi liên quan
Bài 4:
Cho x là số thực dương thoả mãn điều kiện x2 + 1/x2 = 11
Tính giá trị biểu thức: B= x5 + 1/x5
Bài 1 : Cho a,b,c là các số hữu tỉ khác 0 sao cho a+b-c/c=a-b+c/b=(-a)+b+c/a
Tính giá trị của biểu thức A=(a+b).(b+c).(c+a)/abc
(LƯU Ý : DẤU / LÀ ...TRÊN.....)
Bài 2 : Cho x,x2,x3,x4,x5,x6 thỏa mãn :
(x2)^2=x1.x3
(x3)^2=x2.x4
(x4)^2=x3.x5
(x5)^2=x4.x6
Chứng minh rằng : x1/x6=(x1+x2+x3+x4+x5/x2+x3+x4+x5+x6)^5
Giusp mk vs nhé các bn !!!
xét các số nguyên x1;x2;...;x5 thỏa mãn (1 + x1)(1 + x2)···(1 + x5) = (1−x1)(1−x2)···(1−x5) = x. chứng minh rằng xx1x2...x5=0
Đề bài:
Trong trường hợp này, trong tích \(P = \left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots\), sẽ có một thừa số bằng 0.
⇒ \(x = 0\).
Do đó \(x x_{1} x_{2} \hdots x_{5} = 0\).Nếu có một \(x_{i} = - 1\), tương tự, \(x = 0\).
⇒ Kết quả đúng.Nếu không có số nào bằng \(\pm 1\):
Khi đó (1) hoàn toàn xác định.
Lưu ý rằng \(\frac{1 + x_{i}}{1 - x_{i}}\) là một phân số không bằng 0.
Tích của 5 phân số bằng 1.
⇒ Có thể xảy ra, nhưng ta cần liên hệ với tích \(P Q\):
\(P Q = P^{2} = x^{2} = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Nếu không có số nào bằng \(\pm 1\), thì mỗi \(1 - x_{i}^{2} \neq 0\). Vế phải khác 0, suy ra \(x \neq 0\).
Nhưng khi đó \(x^{2} = \prod \left(\right. 1 - x_{i}^{2} \left.\right)\).
Nghĩa là \(x\) chia hết cho tích \(\prod x_{i}\) (do đồng dư mod \(x_{i}\), lập luận chia hết)…
Kết quả là hoặc \(x = 0\) hoặc một trong các \(x_{i} = 0\).
⇒ Trong cả hai trường hợp, \(x x_{1} x_{2} \hdots x_{5} = 0\).Kết luận:
Xét các số nguyên \(x_{1} , x_{2} , \ldots , x_{5}\) thỏa mãn
\(\left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots \left(\right. 1 + x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } \left(\right. 1 - x_{1} \left.\right) \left(\right. 1 - x_{2} \left.\right) \hdots \left(\right. 1 - x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } x .\)
Chứng minh rằng
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
Lời giải:Gọi
\(P = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) , Q = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Theo đề: \(P = Q = x\).
Bước 1: Xét tích \(P Q\)\(P Q = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) \left(\right. 1 - x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Bước 2: Sử dụng giả thiết \(P = Q\)Từ \(P = Q\), suy ra:
\(\prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Chuyển vế:
\(& \prod_{i = 1}^{5} \frac{1 + x_{i}}{1 - x_{i}} = 1. & & (\text{1})\)
Bước 3: Phân tích trường hợpNếu có một \(x_{i} = 1\), thì vế phải (1) có mẫu số bằng 0 → đẳng thức chỉ đúng khi đồng thời tử số cũng bằng 0, tức là có một \(x_{j} = - 1\).Trong trường hợp này, trong tích \(P = \left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots\), sẽ có một thừa số bằng 0.
⇒ \(x = 0\).
Do đó \(x x_{1} x_{2} \hdots x_{5} = 0\).Nếu có một \(x_{i} = - 1\), tương tự, \(x = 0\).
⇒ Kết quả đúng.Nếu không có số nào bằng \(\pm 1\):
Khi đó (1) hoàn toàn xác định.
Lưu ý rằng \(\frac{1 + x_{i}}{1 - x_{i}}\) là một phân số không bằng 0.
Tích của 5 phân số bằng 1.
⇒ Có thể xảy ra, nhưng ta cần liên hệ với tích \(P Q\):
\(P Q = P^{2} = x^{2} = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Nếu không có số nào bằng \(\pm 1\), thì mỗi \(1 - x_{i}^{2} \neq 0\). Vế phải khác 0, suy ra \(x \neq 0\).
Nhưng khi đó \(x^{2} = \prod \left(\right. 1 - x_{i}^{2} \left.\right)\).
Nghĩa là \(x\) chia hết cho tích \(\prod x_{i}\) (do đồng dư mod \(x_{i}\), lập luận chia hết)…
Kết quả là hoặc \(x = 0\) hoặc một trong các \(x_{i} = 0\).
⇒ Trong cả hai trường hợp, \(x x_{1} x_{2} \hdots x_{5} = 0\).Kết luận:
Dù xảy ra trường hợp nào thì ta luôn có:
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
Đúng 0
Bình luận (0)
Xét các số thực x, y thỏa mãn
x
2
+
y
2
≥
4
và
l
o
g
x
2
+
y
2
(
4
x
-
2
y
)
≥
1
. Giá trị lớn nhất của biểu thức P3x+4y-5 là với a, b là các số nguyên. Tính
T
a
3...
Đọc tiếp
Xét các số thực x, y thỏa mãn x 2 + y 2 ≥ 4 và l o g x 2 + y 2 ( 4 x - 2 y ) ≥ 1 . Giá trị lớn nhất của biểu thức P=3x+4y-5 là với a, b là các số nguyên. Tính T = a 3 + b 3
A. 0
B. 250
C. 152
D. 98
Cho hai số thực x, y thỏa mãn
x
2
-
y
2
+
1
2
+
4
x
2
y
2
-
x
2
-
y
2
0
. Gọi...
Đọc tiếp
Cho hai số thực x, y thỏa mãn x 2 - y 2 + 1 2 + 4 x 2 y 2 - x 2 - y 2 = 0 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = x 2 + y 2 . Tính M + m
A. M + m = 3
B. M + m = 5
C. M + m = 2
D. M + m = 4
P(x) = x
5 +x
4 −4x
3 +x
2 −x−2 có hai nghiệm thực a,b thỏa mãn a+b = 1. Tính tích ab?
Bạn vui lòng gõ lại biểu thức $P(x)$ để được hỗ trợ tốt hơn.
Đúng 1
Bình luận (0)
Cho hai số thực dương x, y thỏa mãn: x + y = 5. Tìm gần đúng giá trị nhỏ nhất của biểu thức: P=(x5+5)(y5+5) (Làm tròn kết quả đến 5 chữ số ở phần thập phân)
Cho 2 số thực x ; y thỏa mãn 0 < x ≤ 1 , 0 < y ≤ 1 và x + y = 3xy . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x2 + y2 - 4xy
Cho hai số thực x, y thỏa mãn
x
2
+
y
2
-
4
x
+
6
y
+
4
+
y
2
+
6
y
+
10
6
+
4
x
-
x
2...
Đọc tiếp
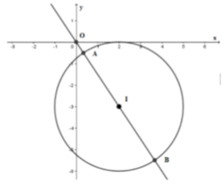
Cho hai số thực x, y thỏa mãn x 2 + y 2 - 4 x + 6 y + 4 + y 2 + 6 y + 10 = 6 + 4 x - x 2 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức T = x 2 + y 2 - a . Có bao nhiêu giá trị nguyên thuộc đoạn [-10;10] của tham số a để M ≥ 2 m
A. 17
B. 16
C. 15
D. 18
Chọn B.
Phương pháp:
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
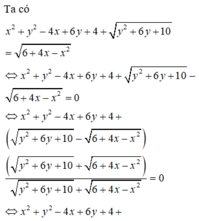
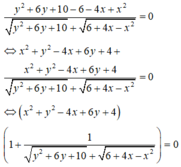


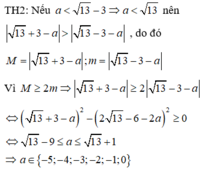

Đúng 0
Bình luận (0)














