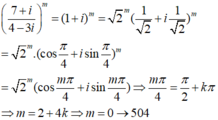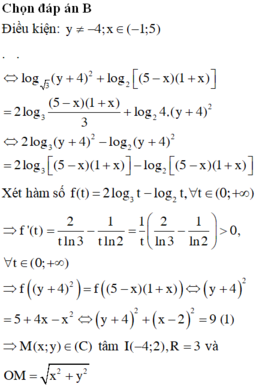tìm số nguyên dương x,y không vượt quá 10 thỏa mãn 4x-3y=17

Những câu hỏi liên quan
Tìm các số nguyên dương x,y không vượt quá 10 thỏa mãn 4x-3y=17
có thể trả lời rõ hơn đc k cách làm để ra kết quả đó ấy
Đúng 0
Bình luận (0)
Tìm các số nguyên dương x , y không vư¤t quá 10 thỏa mãn 4x-3y=17
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Có bao nhiêu số nguyên dương m không vượt quá 2018 thỏa mãn 7 + i 4 − 3 i m là số thuần ảo?
A. 504.
B. 505.
C. 2017.
D. 2018.
Có bao nhiêu số nguyên dương m không vượt quá 2018 thỏa mãn
7
+
i
4
−
3
i
m
là số thuần ảo? A. 504. B. 505. C. 2017. D. 2018.
Đọc tiếp
Có bao nhiêu số nguyên dương m không vượt quá 2018 thỏa mãn 7 + i 4 − 3 i m là số thuần ảo?
A. 504.
B. 505.
C. 2017.
D. 2018.
Tìm các số nguyên dương n không lớn hơn 2015 thỏa mãn [n/2]+[n/3]+[n/4]=n/2+n/3+n/4 ( kí hiệu [a] là số nguyên lớn nhất không vượt quá a)
Ta có: \(\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\left[\frac{n}{4}\right]=\frac{n}{2}+\frac{n}{3}+\frac{n}{4}\)
Mà \(\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\left[\frac{n}{4}\right]\) có kết quả là số nguyên
Nên \(\frac{n}{2}+\frac{n}{3}+\frac{n}{4}\) cũng phải có kết quả là số nguyên. Hay \(\frac{n}{2};\frac{n}{3};\frac{n}{4}\) đều là số nguyên.
=> n chia hết cho cả 2;3 và 4
Vậy n sẽ là Bội của 2;3;4 hay n = 24k (k \(\in\) N*, k < 84) (BCNN(2;3;4)=24)
\(n\in\left\{24;48;72;96;120;...;1992\right\}\) Không có số 0 vì số 0 không phải là số nguyên dương.
Đúng 0
Bình luận (0)
1)số nguyên lớn nhất không vượt quá -64/13
2) số các cặp số nguyên (x,y) thỏa mãn x+y+xy=3 là số nào
1) Ta co: -64 :3 = -21,(3) => so nguyen lon nhat ko vuot qua -21,(3) la -21
Đúng 0
Bình luận (0)
x+y+xy=3 <=>(x+xy)+y=3 <=> x(y+1)+(y+1)=4 <=>(x+1).(y+1)=4 . Ma x,y€Z suy ra x+1, y+1 €Z suy ra x+1,y+1 thuoc uoc cua 4. Ta co bang sau:
| x+1 | 1 | 4 | (-1) | -4 | 2 | -2 | |
| y+1 | 4 | 1 | -4 | (-1) | 2 | -2 | |
| x | 0 | 3 | -2 | -5 | 1 | -3 | |
| y | 3 | 0 | -5 | -2 | 1 | -3 | |
| Danh gia | chon | chon | chon | chon | chon | chon |
Đúng 0
Bình luận (0)
Cho hai số thực x, y thỏa mãn:
log
3
(
y
2
+
8
y
+
16
)
+
l
o
g
2
[(
5
−
x
)
(
1
+
x
)
]2log
3
5
+
4
x...
Đọc tiếp
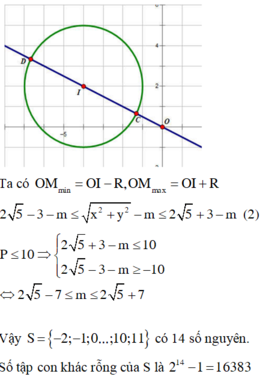
Cho hai số thực x, y thỏa mãn: log 3 ( y 2 + 8 y + 16 ) + l o g 2 [( 5 − x ) ( 1 + x ) ]=2log 3 5 + 4 x − x 2 3 + log 2 ( 2 y + 8 ) 2 . Gọi S là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức P = x 2 + y 2 − m không vượt quá 10. Hỏi S có bao nhiêu tập con không phải là tập rỗng?
A. 2047
B. 16383
C. 16384
D. 32