Cho AHC có 3 góc nhọn , đường cao HE . Trên đoạn HE lấy điểm B sao cho
tia CB vuông góc với AH , hai trung tuyến AM và BK của ABC cắt nhau ở I.
Hai trung trực của các đoạn thẳng AC và BC cắt nhau tại O.
a, Chứng minh ABH ~ MKO
Cho AHC có 3 góc nhọn , đường cao HE . Trên đoạn HE lấy điểm B sao cho
tia CB vuông góc với AH , hai trung tuyến AM và BK của ABC cắt nhau ở I.
Hai trung trực của các đoạn thẳng AC và BC cắt nhau tại O.
a, Chứng minh ABH ~ MKO
Cho tam giác AHC nhọn, đường cao HE. Trên HE lấy điểm B sao cho CB vuồn góc với AH, Trung tuyến AM, BK trong tam giác của tam giác ABC cắt nhau tại I. 2 đường trung trực của đoạn thẳng AC, BC cắt nhau tại O.
a, Chứng minh tam giác ABH đồng dạng với tam giác MKO.
b, CM \(\frac{IO^3+IK^3+IM^3}{IA^3+IH^3+IB^3}=\frac{1}{8}\)
cho tam giác AHC có 3 góc nhọn, đường cao HE, trên đoạn HE lấy điểm B sao cho tia CB vuông góc với AH. hai trung tuyến AM và BK của tam giác ABC cắt nhau ở I. Hai trung trực của các đoạn thẳng AC và BC cắt nhau tại O.
a, CM tam giác ABH ~ tam giác MKO
b, CM \(\sqrt{\dfrac{IO^3+IK^3+IM^3}{IA^3+IH^3+IB^3}}=\dfrac{\sqrt{2}}{4}\)
Cho tam giác vuông ABC vuông tại A, với AC<AB, AH là đường cao kẻ từ đỉnh A. Các tiếp tuyến tại A và B với đường tròn (O) ngoại tiếp tam giác ABC cắt nhau tại M. Đoạn MO cắt cạnh AB ở E. Đoạn MC cắt đường cao AH tại F. Kéo dài CA cắt đường thẳng BM ở D. Đường thẳng BF cắt đường thẳng AM ở N.
(1. C/m OM//CD và M là trung điểm của BD)
2. C/m EF//BC
3, C/m HA là tia phân giác góc MHN
4, Trên tia BA lấy điểm K sao cho BK=3.BA. Kẻ đường thẳng Ky vuông góc với KC tại K cắt BD tại G. C/m tam giác AKG cân.
cho tam giác ABC có 3 góc đều nhọn và đường cao AH. Dựng điểm D sao cho AB là đường trung trực xủa đoạn thẳng HD rồi dựng điểm E sao cho AC là đường trung trực của đoạn thẳng HE. Nối DE cắt AB ở I và cắt AC tại K. CMR a) AD = AE b) tia HA là tia phân giác của góc IHK
Các bạn vẽ hình giúp minh nhá!
Cho tam giác ABC có ba góc nhọn , đường cao AH. Dựng các điểm D và E sao cho AB là đường trung trực của HD, AC là đường trung trực của HE. Đoạn thẳng DE cắt AB tại I, cắt AC tại K . Chứng minh rằng : HA là tia phân giác của góc IKH
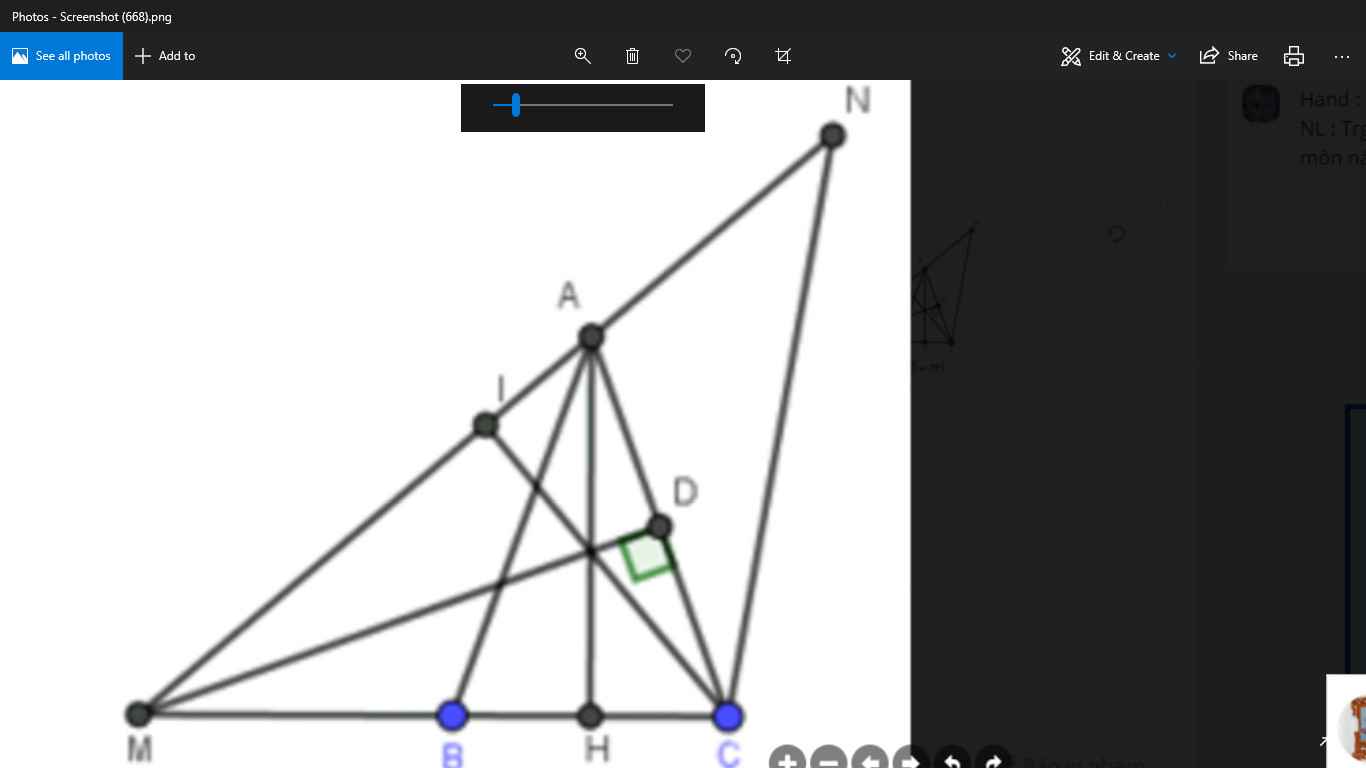
Cho tam giác AHC nhọn, 2 đường cao HE và CF cắt nhau tại B. Trung tuyến AM và BK của tam giác ABC cắt nhau tại I, đường trung trực của AC và BC cắt nhau tại O. C/m:\(\sqrt{\frac{IO^3+IK^3+IM^3}{IA^3+IH^3+IB^3}}=\frac{\sqrt{2}}{4}\)
Cho tam giác ABC có 3 góc đều nhọn và đường cao AH. Dựng điểm D sao cho AB là đường trung trực của đoạn thẳng HD rồi dựng điểm E sao cho AC là đường trung trực của đoạn thẳng HE. Nối DE cắt AB ở I và cắt AC ở K. CMR:
a) AD=AE
nếu biết thì cm luôn
Tia HA là tia pg của góc IHK
Áp dụng : Trường hợp bằng nhau thứ 2 của tam giác
Cho ∆ABC có A= 40°, AB=AC. Gọi H là trung điểm của BC
a, Tính góc ABC, góc ACB và c/m AH vuông góc với BC
b, Trung trực của đoạn thẳng AC cắt tia CB tại M. Tính góc MAH
c, Trên tia đối của tia AM lấy N sao cho AN=BM. CMR: AM=CN
d, Vẽ CI vuông góc với MN tại I. C/m I là trung điểm của MN
a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
\(\text{a)}\Delta ABC\text{ cân tại }A\text{ có }\widehat{A}=40^0\)
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
\(\text{Xét }\Delta ABH\text{ và }\Delta ACH\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
\(BH=CH\text{(H là trung điểm BC)}\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{ÂHB}=\widehat{AHC}\)
\(\text{mà }\widehat{AHB}+\widehat{AHC}=180^0\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\)
\(\Rightarrow AH\perp BC\)
\(\text{b)}\Delta AMC\text{ cân tại M}\text{ vì MD là đường trung trực}\)
\(\Rightarrow\widehat{MAD}=\widehat{MCD}=70^0\)
\(\text{Ta có:}\widehat{MAD}=\widehat{MAH}+\widehat{CAH}\)
\(\Rightarrow\widehat{MAH}=\widehat{MAD}-\widehat{CAH}=70^0-\dfrac{40^0}{2}=50^0\text{(vì AH là phân giác }\widehat{BAC}\text{)}\)
\(\text{c)Xét }\Delta ABM\text{ và }\Delta CAN\text{ có:}\)
\(BM=AN\text{(cách lấy điểm N)}\)
\(AB=AC\left(cmt\right)\)
\(\widehat{ABM}=\widehat{CAN}=180^0-70^0=110^0\)
\(\Rightarrow\Delta ABM=\Delta CAN\left(c.g.c\right)\)
\(\Rightarrow AM=AN\text{(hai cạnh tương ứng)}\)
\(\text{d)Xét }\Delta MIC\text{ và }\Delta NIC\text{ có:}\)
\(IC\text{ cạnh chung}\)
\(\widehat{MIC}=\widehat{NIC}=90^0\)
\(\widehat{IMC}=\widehat{INC}\text{(vì }\Delta ABM=\Delta CAN\text{)}\)
\(\Rightarrow\Delta MIC=\Delta NIC\left(gn.cgv\right)\)
\(\Rightarrow MI=NI\)
\(\Rightarrow\text{I là trung điểm MN}\)