hình thang có thêm điều kiện gì để thành hình bình hành

Những câu hỏi liên quan
Hình bình hành cần thêm điều kiện gì để trở thành hình vuông A. Hai đường chéo bằng nhau; B. Hai đường chéo cắt nhau tại trung điểm mỗi đường; C. Hai cạnh kề bằng nhau; D. Có một góc vuông và hai đường chéo vuông góc với nhau.
Đọc tiếp
Hình bình hành cần thêm điều kiện gì để trở thành hình vuông
A. Hai đường chéo bằng nhau;
B. Hai đường chéo cắt nhau tại trung điểm mỗi đường;
C. Hai cạnh kề bằng nhau;
D. Có một góc vuông và hai đường chéo vuông góc với nhau.
hình thang vuông có thêm điều kiện gì để thành hình chữ nhật
Một hình thang vuông có hai cạnh bên song song là hình chữ nhật
Đúng 0
Bình luận (0)
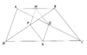
Cho hình thang ABCD gọi M, N, P, Q lần lượt là trung điểm của hai đáy và hai đường chéo của hình thang.
a) Chứng minh rằng tứ giác MPNQ là hình bình hành.
b) Hình thang ABCD phải có thêm điều kiện gì để tứ giác MPNQ là hình thoi?
a) Áp dụng tính chất đường trung bình của tam giác cho DABC và DDBC ta sẽ có:
MQ//PN//BC và MQ = PN = 0.5BC ÞMPNQ là hình bình hành.
b) Tương tự ta có QN//MP//AD và QN = MP = 0.5AD.
Nên để MPNQ là hình thoi thì MN ^ PQ khi đó MN ^ CD và trung trực hay trục đối xứng của AB và CD.
Þ hình thang ABCD là hình thang cân
Đúng 0
Bình luận (0)
a, Hình thoi có phải là hình bình hành không?
b, Hình bình hành cần điều kiện gì để trở thành hình thoi?
Giúp mình với
a, Hình thoi là hình bình hành, vì hình thoi là tứ giác có hai cặp cạnh đối diện song song và bằng nhau
b, Hình bình hành muốn trở thành hình thoi thì hình bình hình phải có hai cạnh bên bằng nhau
Đúng 0
Bình luận (0)
a, Không, hình thời không phải là hình bình hành. Hình bình hành có các bài hát cạnh nhau và bằng nhau, trong khi hình thời có các bài hát cạnh nhau nhưng không có bài hát.
b, Để trở thành hình thoi, hình bình hành cần đáp ứng các điều kiện sau:
- Có 2 Liền kề nhau và song song.
- Có 4 góc vuông.
- Có 2 đường chéo nhau cắt góc và chia đôi hình bình hành.
Đúng 0
Bình luận (0)
THAM KHẢO Ý MK VÀ CHỊ GG NHÉ:
Hình thoi là hình bình hành nha! Lý do vì :
1. hình thoi là tứ giác có hai cặp cạnh đối diện song song và bằng nhau
Nhớ thêm: hình thoi đảo ngược lại sẽ là hình vuông, mà zuông thì khá giống hình bình hành(cái này ko có khoa học lắm, theo cách đơn giản thui)
Để chứng minh dễ hiểu hơn thì đây:
Hình thoi là một dạng đặc biệt của một hình bình hành vì nó có đầy đủ tính chất của hình bình hành và còn có một số tính chất khác: Hình bình hành có hai cạnh kề bằng nhau là hình thoi. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho hình thang ABCD gọi M,N,.P,Q lần lượt là trung điểm của AB,BC,CD,AD
a)CM: tứ giác MNPQ là hình bình hành
b)hình thang ABCD có thêm điều kiện gì để MNPQ là hình chữ nhật
a
Do:
MQ là đường trung bình của tam giác ABD nên MQ//BD và MQ=BD/2 (1)
NP là đường trung bình của tam giác CBD nên NP//BD và NP=BD/2 (2)
Từ (1) và (2) suy ra điều phải chứng minh ( có 2 cặp cạnh đối song song và bằng nhau )
b
MNPQ là hình chữ nhật nên QM vuông góc với MN.
Khi đó AC vuông góc với BD.
Vậy hình thang ABCD cần thêm điều kiện AC vuông góc với BD thì MNPQ là hình chữ nhật.
Đúng 1
Bình luận (0)
Cho tam giác ABC .Goi M,N,P theo thứ tự là trung điểm cua BC,AC,AB.Qua A vẽ đường thẳng song song với BC cat MN tai Qa.chứng minh tứ giác BCNQ là hình thangb.chứng minh tứ giác ABNQlà hình bình hànhc.tìm điều kiện cua tam giác ABC để tứ giác ABMQ là hình chữ nhậtd. chứng minh tứ giác APMN là hình bình hànhe.để tứ giác APMN là hình thoi thì tam giác ABC hải có thêm điều kiện gìf.chứng minh tứ giác AMCQ là hình bình hành.Tam giác ABC cần thêm điều kiện gì để tứ giác AMCQ là hình chữ nhật
Đọc tiếp
Cho tam giác ABC .Goi M,N,P theo thứ tự là trung điểm cua BC,AC,AB.Qua A vẽ đường thẳng song song với BC cat MN tai Q
a.chứng minh tứ giác BCNQ là hình thang
b.chứng minh tứ giác ABNQlà hình bình hành
c.tìm điều kiện cua tam giác ABC để tứ giác ABMQ là hình chữ nhật
d. chứng minh tứ giác APMN là hình bình hành
e.để tứ giác APMN là hình thoi thì tam giác ABC hải có thêm điều kiện gì
f.chứng minh tứ giác AMCQ là hình bình hành.Tam giác ABC cần thêm điều kiện gì để tứ giác AMCQ là hình chữ nhật
Cho hình bình hành ABCD. Các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH.
a) Tứ giác EFGH là hình gì ? Vì sao ?
b) Chứng minh rằng EG = FH và bằng hiệu giữa hai cạnh kề một đỉnh của hình bình hành ABCD.
c) Hình bình hành ABCD cần có thêm điều kiện gì để EFGH là hình vuông?
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM=DN. Đường trung trực của BM lần lượt cắt các đương thẳng MN và BC tại E và F. Hình bình hành ABCD phải có thêm điều kiện gì để tứ giác BCNE là hình thang cân?
Cho hình thang ABCD (AB//CD). gỌI E , F theo thứ tự là trung điểm AB , CĐ . gỌI O là trung điểm EF. Qua O kẻ đường thẳng song song với AB cắt AD và BC theo thứ tự tại M,Na) Tứ giác EMFN là hình gì DS : EMFN là hình bình hànhb) Hình thang ABCD có thêm điều kiện để EMFN là hình thoi DS : ABCD là hình thang cânc)Hình thang ABCD có thêm điều kiện gì để EMFN là hình vuông DS ABCD là hình thang cân và có 2 đường chéo vuông góc
Đọc tiếp
Cho hình thang ABCD (AB//CD). gỌI E , F theo thứ tự là trung điểm AB , CĐ . gỌI O là trung điểm EF. Qua O kẻ đường thẳng song song với AB cắt AD và BC theo thứ tự tại M,N
a) Tứ giác EMFN là hình gì DS : EMFN là hình bình hành
b) Hình thang ABCD có thêm điều kiện để EMFN là hình thoi DS : ABCD là hình thang cân
c)Hình thang ABCD có thêm điều kiện gì để EMFN là hình vuông DS ABCD là hình thang cân và có 2 đường chéo vuông góc
a) XÉT HÌNH THANG AEDF(AE//DF) O LÀ TRUNG ĐIỂM EF, OM//DF=> M PHẢI LÀ TĐ CỦA AD
TƯƠNG TỰ C/M N LÀ TĐ BC
ĐẾN ĐÂY LÀM GIỐNG BÀI HÔM TRC ĐÓ E. KẺ 2 ĐƯỜNG CHÉO AC,DB
TAM GIÁC ADB: E,M LÀ TRUNG ĐIỂM 2 CẠNH BÊN => EM LÀ ĐTB => EM//DB. TƯƠNG TỰ VỚI TAM GIÁC DBC:... => FN//DB
=> EM//FN.
TƯƠNG TỰ C/M: EN//MF => TỨ GIÁC EMFN LÀ HÌNH BÌNH HÀNH
B) EMFN LÀ HÌNH THOI <=> EM=EN. MÀ EM=1/2 DB; EN=1/2 AC => AC=DB => HÌNH THANG ABCD CÂN
C) EMFN LÀ HÌNH VUÔNG <=> EMFN LÀ HÌNH THOI (ĐK CÂU B) VÀ EM VUÔNG GÓC EN TẠI E. MÀ EM//DB, EN//AC => DB VUÔNG GÓC AC
=> ABCD là hình thang cân và có 2 đường chéo vuông góc
Đúng 1
Bình luận (0)
123 + 345 = 468
468 + 567 = 1035
1035 - 236 = 799
799 - 189 = 610
610 + 853 = 1463
Đúng 0
Bình luận (0)


















