Nêu các cách chứng minh 2 đường thẳng vuông góc.
Câu 10: Phát biểu tiên đề Euclid.
Câu 11: Nêu định lí tổng các góc trong tam giác.
Câu 12: Nêu các trường hợp bằng nhau của tam giác thường, tam giác vuông?
Câu 13: Nêu một số cách chứng minh đoạn thẳng bằng nhau, góc bằng nhau, đường thẳng vuông góc, tam giác cân, tam giác đều, 3 điểm thẳng hàng.
Câu 14: nêu các đường đồng qui trong tam giác và tính chất của chúng?
Câu 15: Nêu các công thức tính diện tích xung quanh, diện tích toàn phần, thể tích của hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác.
`@` `\text {Ans}`
`\downarrow`
`10,`
`@` Tiên đề Euclid được phát biểu như sau:
`-` Qua một điểm nằm ngoài 1 đường thẳng, chỉ có duy nhất `1` đường thẳng song song với đường thẳng đó.
`11,`
Định lý tổng `3` góc trong `1` `\triangle`
`-` Trong `1` `\triangle`, tổng số đo của `3` góc là `180^0`
`12,`
Các TH bằng nhau của `\triangle` thường:
`+` Cạnh - Cạnh - Cạnh
`+` Cạnh - Góc - Cạnh
`+` Góc - Cạnh - Góc
Các TH bằng nhau của `\triangle` vuông:
`+` Cạnh - Góc - Cạnh
`+` Góc - Cạnh - Góc
`+` Cạnh huyền - Góc vuông
`+` Cạnh góc vuông - Góc nhọn
`+` Cạnh huyền - Cạnh góc vuông
`+` Hai cạnh góc vuông
15:
Hình hộp chữ nhật
Sxq=(a+b)*2*h
Stp=Sxq+2*a*b
V=a*b*h
Hình lập phương
Sxq=a^2*4
Stp=a^2*6
V=a^3
Hình lăng trụ đứng tam giác
Sxq=C đáy*h
Stp=Sxq+2*S đáy
14:
Các đừog đồng quy là các đường cao, các đường trung tuyến, các đường phân giác, các đường trung trực
Các đường cao thì cắt nhau ở trực tâm của tam giác
Các đường trung tuyến thì cắt nhau ở trọng tâm của tam giác
Các đường phân giác thì cắt nhau ở tâm đừog tròn nội tiếp của tam giác
Các đường trung trực thì cắt nhau ở tâm đường tròn ngoại tiếp của tam giác
10:
Qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng đi qua nó và song song với đường thẳng đã cho
11:
Tổng ba góc trong một tam giác bằng 180 độ
`13,`
`@` 1 số cách c/m 2 đt' bằng nhau:
`+` Sử dụng tính chất của trung điểm
`+` Hai cạnh tương ứng trong `2` `\triangle` bằng nhau
`+` Hai cạnh bên của `\triangle` cân
`+` Sử dụng t/c của đường trung tuyến trong `\triangle` vuông (kì `2` lớp 7 mới)
`+` Tính chất của điểm nằm trên đường trung trực.
`@` 1 số cách c/m 2 góc bằng nhau:
`+` Hai góc tương ứng trong `2` `\triangle` `=` nhau
`+` Sử dụng t/c đường phân giác
`+` Sử dụng t/c của tiên đề Euclid (khi `2` đt' // thì các cặp góc sole trong bằng nhau, các cặp góc đồng vị bằng nhau)
`+` Hai góc đối đỉnh thì bằng nhau
`+`...
`@` 1 số cách c/m đường thẳng vuông góc:
`+` Chứng minh góc đó `= 90^0`
`+` T/c đường trực tâm của `\triangle` (kì 2 lớp 7)
`+` `2` đt' đó có chứa `2` tia phân giác của `2` góc kề bù
`+`...
`@` 1 số cách c/m tam giác cân:
`+` Chứng minh `2` cạnh bên bằng nhau
`+` Chứng minh `2` góc ở đáy bằng nhau
`+` T/c của các đường trong `\triangle` với `\triangle` cân
`@` 1 số cách c/m `3` điểm thẳng hàng:
`+` Chứng minh góc bẹt (tổng số đo của các góc trên đt' đó `= 180^0`)
`+` Chứng minh `3` điểm đó cùng thuộc `1` đt'
Cho hình lập phương ABCD.A'B'C'D' như hình vẽ.
a) Nêu vị trí tương đối của các cặp đường thẳng BC' và A'D'; DD' và AB; AA’ và A’C'.
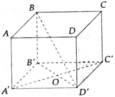
b) Chứng minh A'C' vuông góc với (BB'D'). Từ đó chứng minh A'C' vuông góc BD'.
c) Chứng minh B O = B B ' + 1 4 B ' A ' 2 + B ' C ' 2
Các cách chứng minh 2 đường thẳng vuông góc.
muốn cm 2 đường thẳng vuông gọc ta chứng minh có 1 góc tạo thành bằng 90 đọ
chúc bạn học tốt
^_^ !
18 PHƯƠNG PHÁP CHỨNG MINH HAI ĐƯỜNG THẲNG VUÔNG GÓC
cho góc XOY, điểm thuộc tia phân giác của góc. qua m, kẻ đường thẳng vuông góc ox tại A, cắt ox tại C. qua m, kẻ đường thẳng vuông góc tại B cắt ox tại điểm d
A) chứng minh: OA=OB
B) chứng minh: Om là đường trung trực AB
C) tìm tập hợp các điểm cách đều O và C
D) chưng minh: AB//DC
E) qua D, kẻ đường thẳng A vuông góc OX, đường thẳng B vuông góc OY, N là giao điểm của a và b.
chứng minh: o,m,n thẳng hàng
Nêu các cách chứng minh 2 đường thẳng song song
Cho hình vuông ABCD. Dựng đoạn AS vuông góc với mặt phẳng chứa hình vuông ABCD.
a) Hãy nêu tên các mặt phẳng lần lượt chứa các đường thẳng SB, SC, SD và vuông góc với mặt phẳng (ABCD)
b) Chứng minh rằng mặt phẳng (SAC) vuông góc với mặt phẳng (SBD)
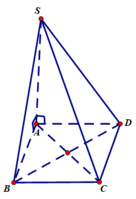
a) SA ⊥ (ABCD), SA ⊂ (SAB) ⇒ (SAB) ⊥ (ABCD)
SA ⊥ (ABCD), SA ⊂ (SAD) ⇒ (SAD) ⊥ (ABCD)
SA ⊥ (ABCD)⇒SA ⊥ BD ⊂(ABCD) và BD ⊥ AC(hai đường chéo hình vuông)
⇒BD ⊥ (SA,AC)⇒BD ⊥ (SAC) mà BD ⊂(ABCD) nên (SAC) ⊥ (ABCD)
b) BD ⊥ (SAC) mà BD ⊂(SBD) nên (SAC) ⊥ (SBD)
Cho tam giác ABC vuông tại A có AB<AC. Trên cạnh AC lấy điểm H. Qua C kẻ đường thẳng vuông góc với đường thẳng BH tại D.
a) Chứng minh HB.HD=HA.HC
b) Chứng minh tam giác ADH đồng dạng tam giác BCH
c) Kẻ HK vuông góc BC tại K. Chứng minh H cách đều ba cạnh của tam giác ADK.
a) Xét ΔCDH vuông tại D và ΔBAH vuông tại A có
\(\widehat{CHD}=\widehat{BHA}\)(hai góc đối đỉnh)
Do đó: ΔCDH\(\sim\)ΔBAH(g-g)
Suy ra: \(\dfrac{HD}{HA}=\dfrac{HC}{HB}\)
hay \(HB\cdot HD=HA\cdot HC\)
b) Ta có: \(\dfrac{HD}{HA}=\dfrac{HC}{HB}\)(cmt)
nên \(\dfrac{HD}{HC}=\dfrac{HA}{HB}\)
Xét ΔADH và ΔBCH có
\(\dfrac{HD}{HC}=\dfrac{HA}{HB}\)(cmt)
\(\widehat{AHD}=\widehat{BHC}\)(hai góc đối đỉnh)
Do đó: ΔADH\(\sim\)ΔBCH(c-g-c)
1 Nêu tính chất 3 đường trung tuyến , tia phân giác của một góc , đường phân giác của tam giác
2 Nêu cách chứng minh 3 điểm thẳng hàng
Cho đường tròn (O;R) và 1 điểm M cách O một khoảng bằng 2R. Vẽ các tiếp tuyến MA; MB với đường tròn tâm O (B; A là các tiếp điểm).
a, Chứng minh rằng: Góc AMO = 300 và tính AM theo R
b, Chứng minh tam giác ABM đều và tính chu vi tam giác ABM theo R
c, Đường thẳng vuông góc với OB tại O cắt AM tại D. Đường thẳng vuông góc với OA tại O cắt MB tại E. Chứng minh rằng Tứ giác MDOE là hình thoi
d, Chứng minh đường thẳng DE là tiếp tuyến của (O;R)