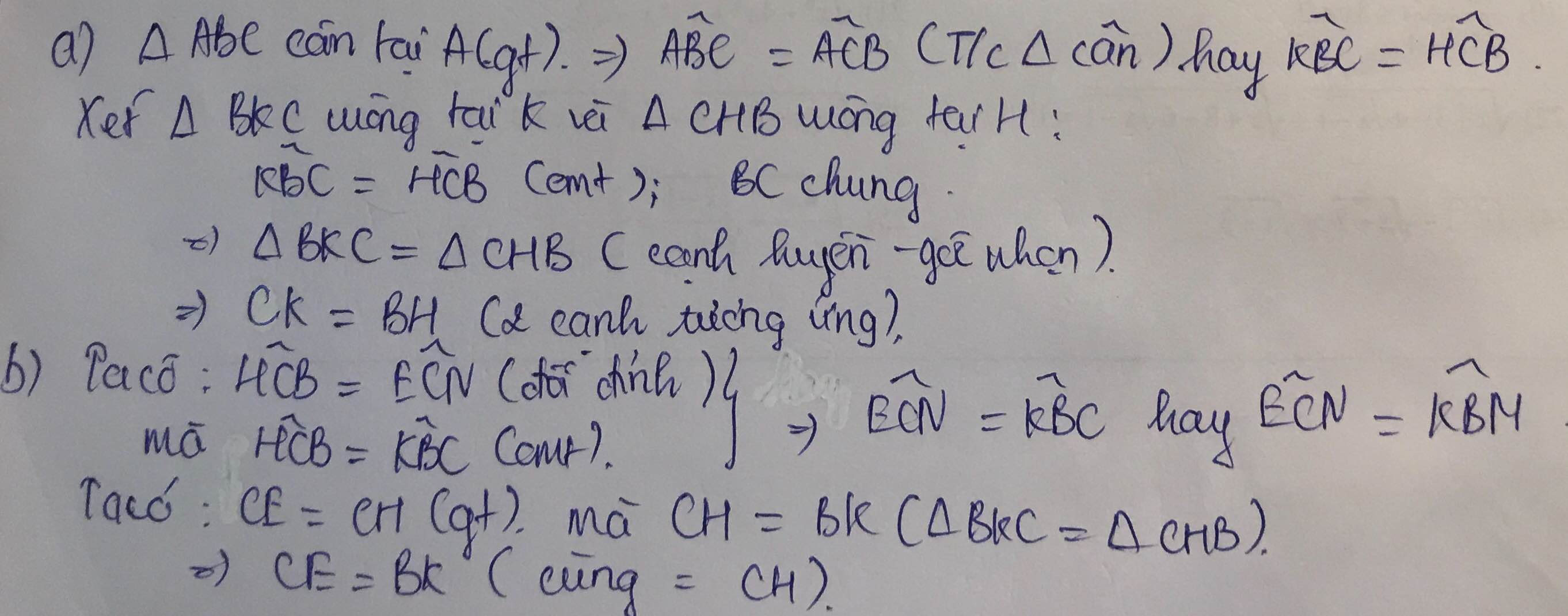cho hình vuông ABCD lấy điểm I trên cạnh BC . Kẻ BH vuông góc với ID ( H thuộc ID ) . Tính góc AHC

Những câu hỏi liên quan
Cho hình vuông ABCD, trên cạnh AB, AD lần lượt lấy điểm I, K sao cho AI = AK. Kẻ AP vuông góc với ID (P thuộc ID). Chứng minh CP vuông góc với KP
Ta có \(\widehat{AIP}=\widehat{DAP}\) (Cùng phụ với góc ADI) nên \(\Delta IAP\sim\Delta ADP\left(g-g\right)\)
\(\Rightarrow\frac{AP}{DP}=\frac{AI}{DA}\Rightarrow\frac{AP}{DP}=\frac{AK}{DC}\)
Lại có \(\widehat{IAD}=\widehat{ADP}\) nên \(\widehat{PAK}=\widehat{PDC}\) (Cùng phụ với hai góc trên)
Vậy nên \(\Delta PAK\sim\Delta PDC\left(c-g-c\right)\)
\(\Rightarrow\widehat{APK}=\widehat{DPC}\)
\(\Rightarrow\widehat{APK}+\widehat{KPD}=\widehat{DPC}+\widehat{KPD}\)
\(\Rightarrow\widehat{APD}=\widehat{KPC}\)
\(\Rightarrow\widehat{KPC}=90^o\)
Vậy nên CP vuông góc KP.
Đúng 0
Bình luận (0)
cho hình vuông ABCD có cạnh bằng a, trên tia đối của tia CD lấy điểm E sao cho CE=a. Gọi N là trung điểm của BE, từ B kẻ BH vuông góc với DN tại H. CMR góc AHC = 90 độ
Bài 2. Cho tam giác ABC vuông tại A. Các tia phân giác của các góc A và B cắt nhau tại I. Kẻ ID vuông góc với AB,IE vuông góc với AC (D thuộc AB,E thuộc AC)a) Chứng minh AD AEb) Trên cạnh BC, lấy điểm H sao cho BH BD. Chứng minh IH vuông góc BCc) Chứng minh CI là tia phân giác của góc ACB . d) Chứng minh (AB+AC-BC) : 2e) Tính độ dài các cạnh BC, ID. Biết rằng AB 6cm, AC 8cm.làm hộ mình vs ạ
Đọc tiếp
Bài 2. Cho tam giác ABC vuông tại A. Các tia phân giác của các góc A và B cắt nhau tại I. Kẻ ID vuông góc với AB,IE vuông góc với AC (D thuộc AB,E thuộc AC)
a) Chứng minh AD = AE
b) Trên cạnh BC, lấy điểm H sao cho BH = BD. Chứng minh IH vuông góc BC
c) Chứng minh CI là tia phân giác của góc ACB .
d) Chứng minh (AB+AC-BC) : 2
e) Tính độ dài các cạnh BC, ID. Biết rằng AB = 6cm, AC = 8cm.
làm hộ mình vs ạ
Cho tam giác ABC cân tại A có 3 góc đề nhọn.
1. Kẻ BH vuông góc với AC tại H,trên cạnh BC lấy điểm I (khác B và C), qua I kẻ DI vuông góc vớiAB, IE vuông góc với AC, Ì vuông góc với BH.
a)Chúng minh tam giác DBI=FIB.
b)Chúng minh ID +IE = BH
2.Phân giác của góc ABC, BKC cắt AC, BC lần lượt tại K, M.Phân giác của góc BKA cắt BC tại N.CMR:BK=1/2MN
cho hình chữ nhật ABCD kẻ AH vuông góc với BD (H thuộc BD). Trên đoạn DH lấy điểm E ,trên cạnh BC lấy điểm F sao cho DE.CBDH.CF.Chứng minh rằng:2BD.BHLớp 8Toán
Đọc tiếp
cho hình chữ nhật ABCD kẻ AH vuông góc với BD (H thuộc BD). Trên đoạn DH lấy điểm E ,trên cạnh BC lấy điểm F sao cho DE.CB=DH.CF.Chứng minh rằng:
2=BD.BH
Lớp 8Toán
Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC, CK vuông góc với AB ( H thuộc AC,K thuộc AB. 1) Chứng minh: BH =CK . 2) Trên tia đối CA lấy điểm E sao cho CE=CH . Kẻ KM vuông góc với BC tại M và EN vuông góc với BC tại N. Gọi I là giao điểm của KE với cạnh BC.Chứng minh EN = KM và I là trung điểm của KE
Cho tam giác ABC cân tại A Trên tia đối của tia BC lấy điểm D Trên tia đối của tia CB lấy điểm E Sao cho BD=CE.Kẻ BH vuông góc AD (H thuộc AD),kẻ CK vuông góc AE (K thuộc AE) a,c/m BH=CK b, c/m tam giác AHB= tam giác AHC c,c/m BC//HK
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: \(\widehat{D}=\widehat{E}\)
Xét ΔHDB vuông tại H và ΔKEC vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHDB=ΔKEC
Suy ra: BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
Do đó: ΔAHB=ΔAKC
Đúng 0
Bình luận (0)
Cho △ABC cân tại A. Kẻ BH vuông góc với AC, CK vuông góc với AB (H ∈ AC, K ∈ AB).
1) Chứng minh: BH = CK.
2) Trên tia đối CA lấy điểm E sao cho CE = CH. Kẻ KM vuông góc với BC tại M và EN vuông góc với BC tại N. Gọi I là giao điểm của KE với cạnh BC.Chứng minh EN = KM và I là trung điểm của KE.
mọi người đừng làm tắt quá nha, mình cảm ơn ạ
1: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
2: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
Suy ra:KB=HC
=>KB=CE
Xét ΔKBM vuông tại M và ΔECN vuông tại N có
KB=EC
\(\widehat{KBM}=\widehat{ECN}\left(=\widehat{ACB}\right)\)
Do đó: ΔKBM=ΔECN
Suy ra: KM=EN
Xét tứ giác KMEN có
KM//EN
KM=EN
Do đó: KMEN là hình bình hành
Suy ra: Hai đường chéo KE và MN cắt nhau tại trung điểm của mỗi đường
hay I là trung điểm của KE
Đúng 2
Bình luận (0)
Cho ΔABC cân tại A. Trên cạnh AB lấy điểm D. Trên tia đối của tai AC lấy điểm E sao cho BD=CE, nối D với E sao cho BD=CE, nối D với E, kẻ DH vuông góc với BC (H thuộc BC), EK vuông góc với BC (K thuộc BC). chứng minh:
a) BH=CK
b) BC<DE
a: Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
BD=CE
góc DBH=góc ECK
=>ΔDHB=ΔEKC
=>BH=CK
b: Tham khảo:

Đúng 0
Bình luận (0)