Nhờ thầy cô và các bạn giúp đỡ

Những câu hỏi liên quan
Nhờ thầy cô và các bạn giúp đỡ
Nhờ thầy cô và các bạn giúp đỡ với ạ
Lời giải:
Gọi số công nhân mỗi đội lần lượt là $a,b,c$. Vì số công nhân tỉ lệ nghịch với số
ngày làm nên $4a=6b=8c=\frac{a}{\frac{1}{4}}=\frac{b}{\frac{1}{6}}=\frac{c}{\frac{1}{8}}$
Áp dụng TCDTSBN:
$\frac{a}{\frac{1}{4}}=\frac{b}{\frac{1}{6}}=\frac{c}{\frac{1}{8}}=\frac{a-b}{\frac{1}{4}-\frac{1}{6}}=\frac{4}{\frac{1}{12}}=48$
$\Rightarrow a=48.\frac{1}{4}=12; b=48.\frac{1}{6}=8; c=48.\frac{1}{8}=6$
Đúng 0
Bình luận (0)
Nhờ thầy cô và các bạn giúp đỡ em với ạ
Đọc tiếp
Nhờ thầy cô và các bạn giúp đỡ em với ạ
Nhờ thầy cô và các bạn trong nhóm giúp đỡ em với ạ!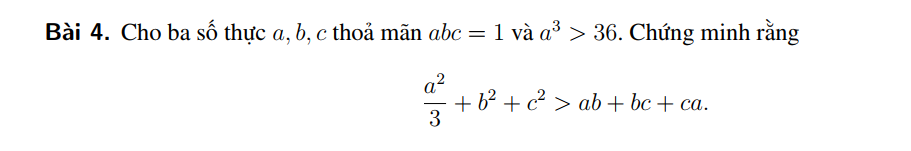
Từ GT \(\Leftrightarrow a>0;bc>0\)
\(BĐT\Leftrightarrow\dfrac{a^2}{3}+\left(b+c\right)^2-3bc-a\left(b+c\right)\ge0\\ \Leftrightarrow\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\ge0\)
Vì \(a^3>36\) nên
\(\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\\ >\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}+\dfrac{1}{4}=\left(\dfrac{b+c}{a}-\dfrac{1}{2}\right)^2\ge0\)
Đúng 2
Bình luận (1)
Nhờ thầy cô giáo và các bạn giúp đỡ theo kiến thức học kì 1 -- Toán Lớp 8 với ạ.
Cám ơn thầy cô nhiều ạ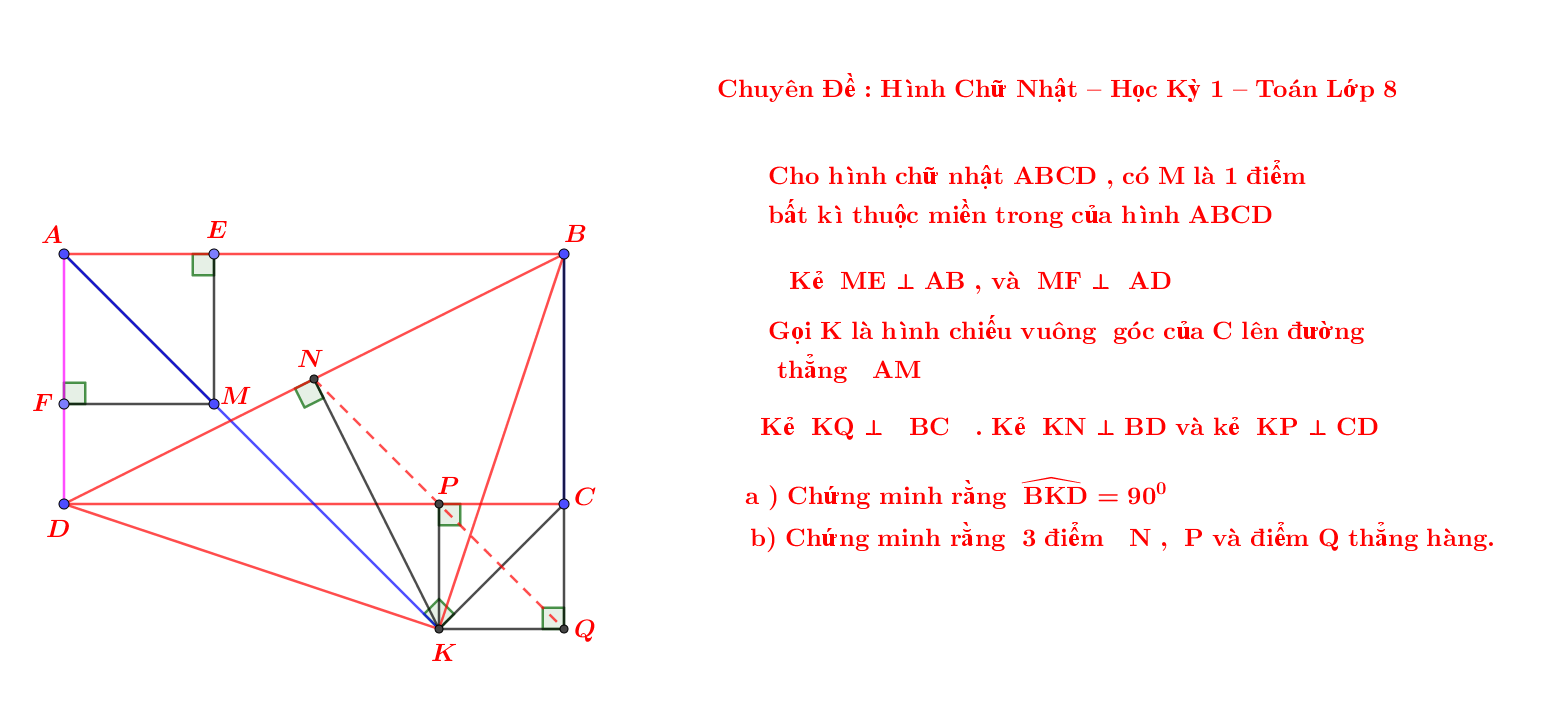
Nhờ thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều ạ!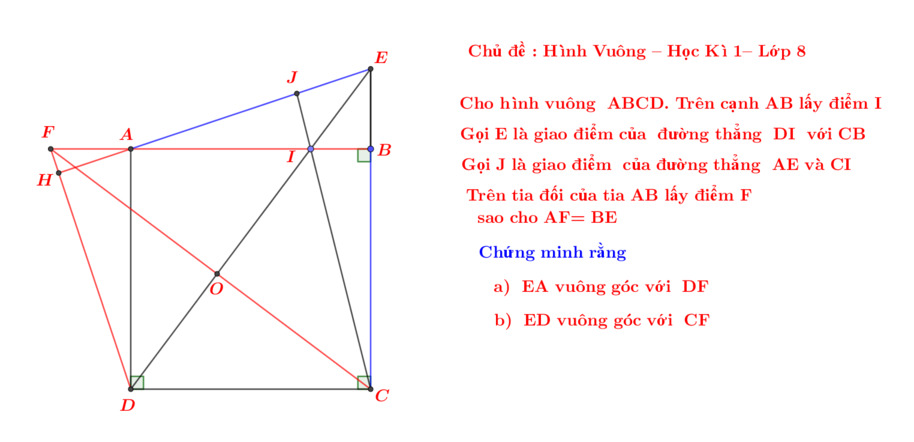
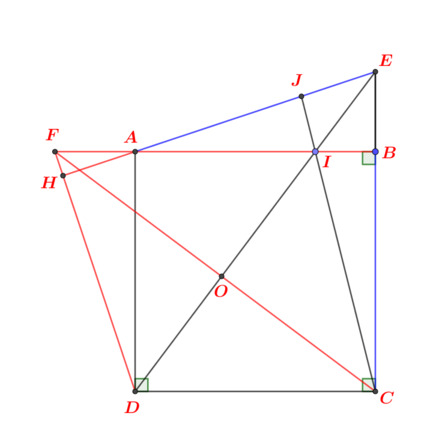
Xin nhờ quý thầy cô và các bạn yêu toán gần xa giúp đỡ với ạ!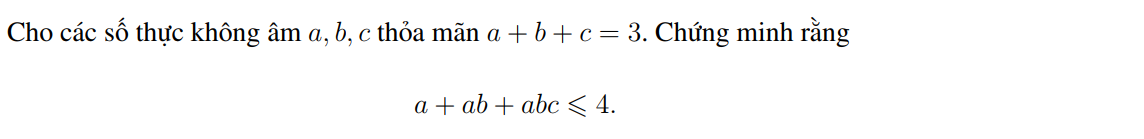
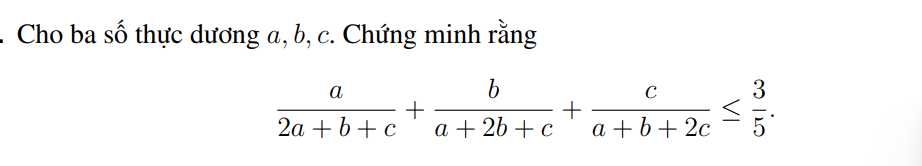
Áp dụng BĐT cosi dạng \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\cdot\dfrac{1}{4}\ge\dfrac{4}{a+b}\cdot\dfrac{1}{4}\\ \Leftrightarrow\dfrac{1}{a+b}\le\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
\(\Leftrightarrow\dfrac{a}{2a+b+c}=\dfrac{a}{a+b+a+c}\le\dfrac{a}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)\)
Cmtt \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{b}{a+2b+c}\le\dfrac{b}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}\right)\\\dfrac{c}{a+b+2c}\le\dfrac{c}{4}\left(\dfrac{1}{a+c}+\dfrac{1}{b+c}\right)\end{matrix}\right.\)
Cộng VTV 3 BĐT trên:
\(\Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}+\dfrac{b}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{a+c}+\dfrac{c}{b+c}\right)\\ \Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{a+c}{a+c}\right)=\dfrac{1}{4}\cdot3=\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow a=b=c\)
Đúng 1
Bình luận (1)
Em xin phép nhờ thầy cô và các bạn giúp đỡ với ạ, em cám ơn nhiều
Xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều





