
Những câu hỏi liên quan
Cho đường tròn (O) đường kính AB , C là 1 điểm thuộc đường tròn (CA
Xem chi tiết
Cho đường tròn (O) có đường kính AB. Điểm C thuộc đường tròn (O) sao cho CA<CB. Kẻ CH⊥AB tại H và OM⊥ BC tại M.
a) Chứng minh: 4 điểm C, H, O, M cùng thuộc một đường tròn
b) Gọi E là trung điểm của CH. Chứng minh: CH.AB = AC.BC và CAE = BAM.
c) Gọi T là giao điểm của hai tia AE và OM. Chứng minh: TC là tiếp tuyến của đường tròn ngoại tiếp
ACHM.
a: Xét tứ giác CHOM có
góc CHO+góc CMO=180 độ
nen CHOM là tứ giác nội tiếp
b: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔCAB vuông tại C co CH là đường cao
nên CH*AB=CA*CB
Đúng 0
Bình luận (0)
cho nủa đường tròn (o,R) dduongf kính ab . lấy 1 điểm c thuộc nửa đường tròn sao cho ca<cb kẻ ch vuông góc vs ab . trên cùng một nửa mặt phẳng bờ ab chứa nửa cắt ca tại tròn vẽ 2 nửa đường tròn tâm o1 đường kính ah o2 đường kính HB (o1) cắt ca tại e (o2) cắt cb tại F
a) chứng minh tứ giác CEHF là hình chữ nhật
Cho đường tròn (O;R) đường kính AB, điểm C thuộc đường tròn (O) sao cho CA < CB. Vẽ dây CD vuông góc với AB tại H. Gọi E là điểm điểm đối xứng với A qua H.
Chứng minh ACED là hình thoi
Cho nửa đường tròn (O; R) đường kính AB. Lấy một điểm C thuộc nửa đường tròn sao cho CA < CB (C khác A). Kẻ CH vuông góc với AB. Đường tròn đường kính CH cắt CA,CB tại D,E
CHứng minh1 : CO vuông góc với DE Chứng minh 2 : AD.DB +AE.EC =AH bình
Cho đường tròn tâm O , đường kính AB 2R . Điểm C nằm giữa hai điểm A và B , vẽ đường tròn tâm I đường kính CA và đường tròn tâm K đường kính CB . Qua C kẻ đường thẳng vuông góc với AB cắt đường tròn tâm O tại D và E đoạn thẳng DA cắt đường tròn tâm Itại M vs DB cắt đường tròn tâm K tại Na) CMR 4 điểm C,M,Đ,N cùng thuộc 1 đường trònb) CMR MN là tiếp tuyến của đường tròn tâm I và Kc) xác định vj trí điểm C trên đường kính AB sao cho tứ giác CMDN có S lớn nhất
Đọc tiếp
Cho đường tròn tâm O , đường kính AB = 2R . Điểm C nằm giữa hai điểm A và B , vẽ đường tròn tâm I đường kính CA và đường tròn tâm K đường kính CB . Qua C kẻ đường thẳng vuông góc với AB cắt đường tròn tâm O tại D và E đoạn thẳng DA cắt đường tròn tâm I
tại M vs DB cắt đường tròn tâm K tại N
a) CMR 4 điểm C,M,Đ,N cùng thuộc 1 đường tròn
b) CMR MN là tiếp tuyến của đường tròn tâm I và K
c) xác định vj trí điểm C trên đường kính AB sao cho tứ giác CMDN có S lớn nhất
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
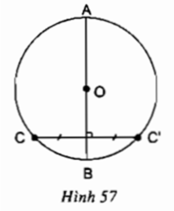
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)
Đúng 0
Bình luận (0)
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
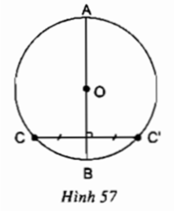
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)
Đúng 0
Bình luận (0)
CHO NỬA đường tròn (o,r) đường kính ab . ấy một điểm c thuộc nủa đường tròn sao cho ca < cb










