giải tam giác ABC biết a = 49,4m , b^ = 26,4m và c^ = 27°20'

Những câu hỏi liên quan
Cho tam giác ABC, biết hiệu của góc A - B=20 độ và hiệu của góc B - C=20 độ. Tính góc A ⏳
(GHI CÁCH GIẢI ĐÀNG HOÀNG)
góc A = 80 độ
đúng thì tick cko mik nha
Đúng 0
Bình luận (0)
Giải các tam giác vuông sau, tầm giác ABC vuông tại A biết: a)a=20;b=16 b)b=10;C=50° c)cos B=3/4;c=5
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB=\sqrt{20^2-16^2}=12\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=40^0\)
Xét ΔABC vuông tại A có
\(tanC=\dfrac{AB}{AC}\)
=>\(AB=10\cdot tan50\simeq11,92\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{10^2+11.92^2}\simeq15,56\left(cm\right)\)
c: Xét ΔABC vuông tại A có \(cosB=\dfrac{3}{4}\)
=>\(\dfrac{AB}{BC}=\dfrac{3}{4}\)
=>\(\dfrac{5}{BC}=\dfrac{3}{4}\)
=>\(BC=\dfrac{20}{3}\)
Xét ΔABC vuông tại A có cosB=3/4
nên \(\widehat{B}\simeq41^0\)
=>\(\widehat{C}=49^0\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{\left(\dfrac{20}{3}\right)^2-5^2}=\dfrac{5\sqrt{7}}{3}\left(cm\right)\)
Đúng 3
Bình luận (0)
a, Theo định lý Pytago :
\(AB^2+AC^2=BC^2\\ \Rightarrow AB=\sqrt{20^2-16^2}=12\)
\(cosB=\dfrac{AB}{BC}=\dfrac{12}{20}\Rightarrow\widehat{B}=53^o8'\)
\(cosC=\dfrac{AC}{BC}=\dfrac{16}{20}\Rightarrow\widehat{C}=36^o52'\)
b, Vì tam giác ABC vuông tại A
\(\widehat{B}+\widehat{C}=90^o\\ \Rightarrow\widehat{B}=90^o-50^o=40^o\)
\(cosC=\dfrac{AC}{BC}\Rightarrow BC=\dfrac{AC}{cosC}=\dfrac{10}{cos50^o}\approx15,6\)
\(tanC=\dfrac{AB}{AC}\Rightarrow AB=tanC\times AC=tan50^o\times10\approx11,9\)
c,
\(cosB=\dfrac{AB}{BC}\\ \Rightarrow BC=\dfrac{AB}{cosB}=\dfrac{5}{\dfrac{3}{4}}=\dfrac{20}{3}\)
Theo định lý Pytago :
\(AB^2+AC^2=BC^2\\ \Rightarrow AC=\sqrt{\left(\dfrac{20}{3}\right)^2-5^2}=\dfrac{5\sqrt{7}}{3}\)
\(cosB=\dfrac{3}{4}\Rightarrow\widehat{B}=41^o25'\\ sinC=\dfrac{AB}{BC}=\dfrac{5}{\dfrac{20}{3}}=48^o35'\)
Đúng 1
Bình luận (0)
1 Giải tam giác vuông ABC biết rằng  900 và :a) b 10 cm, ; b) c 10 cm, ; c) a 20 cm, ; d) c 21 cm, b 18 cm; 2 Cho DABC nhọn có đường cao AH và đường trung tuyến AM. Biết , AB 9 cm, AC 12 cm. Giải tam giác ABC và tính AM.
Đọc tiếp
1 Giải tam giác vuông ABC biết rằng  = 900 và :
a) b = 10 cm, ; b) c = 10 cm, ;
c) a = 20 cm, ; d) c = 21 cm, b = 18 cm;
2 Cho DABC nhọn có đường cao AH và đường trung tuyến AM. Biết , AB = 9 cm, AC = 12 cm. Giải tam giác ABC và tính AM.
Bài 1:
d) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+18^2=765\)
hay \(BC=3\sqrt{85}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{21}{3\sqrt{85}}\)
nên \(\widehat{C}\simeq49^023'\)
\(\Leftrightarrow\widehat{B}=40^037'\)
Đúng 1
Bình luận (0)
Giải tam giác ABC biết : \(a=14;b=18;c=20\)
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{18^2+20^2-14^2}{2\times18\times20}=\dfrac{11}{15}\)
\(\Rightarrow\widehat{A}\approx43^o\)
\(cosB=\dfrac{a^2+c^2-b^2}{2ac}=\dfrac{14^2+20^2-18^2}{2\times14\times20}=\dfrac{17}{35}\)
\(\Rightarrow\widehat{B}\approx61^o\)
Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{C}=180^0-61^o-43^o=76^o\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A. AB = 15 cm, AC = 20 cm. Vẽ tia Ax // BC và tia By vuông góc với BC tại B, tia Ax cắt By tại D.
a) C/m tam giác ABC ~ tam giác DAB
b) Tính BC, DA, DB
c) AB cắt CD tại I. Tính diện tích tam giácBIC
Mình giải được câu a b rồi còn mỗi câu c thôi!! Bạn nào biết giải giúp mình với!! Cảm ơn trước!!! ^-^
Câu 26 . Cho tam giác ABC. Biết A(4;3), trọng tâm G(1;1), trực tâm H( 104/3;-20) XB > 0. Tìm tọa độ hai đỉnh B,CCâu 27. Cho tam giác ABC có A(0; 2), hai đường trung tuyến BM : 4x + 3y – 10 = 0; CN : x – 2 = 0 . Tọa độ các đỉnh B;C là:
Xem chi tiết
Giải tam giác ABC vuông tại A, biết rằng a = 20 cm, B ^ = 35 o
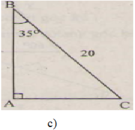
∠B = 90o - ∠C = 90o - 35o = 55o
b = asinB = 20.sin35o ≈ 11,47 (cm)
c = asinC = 20.sin55o ≈ 16,38 (cm)
Đúng 0
Bình luận (0)
Giải tam giác ABC vuông tại A, biết rằng a = 20 c m , B ^ = 35 o
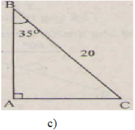
∠B = 90o - ∠C = 90o - 35o = 55o
b = asinB = 20.sin35o ≈ 11,47 (cm)
c = asinC = 20.sin55o ≈ 16,38 (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Kẻ AH vuông BC ( H nằm giữa B và C). Biết AC = 20 cm, AH = 12 cm, BH = 5 cm.
a) Tính chu vi tam giác ABC
b) Tính diện tích tam giác ABC
c) Tam giác ABC có là tam giác vuông không
Hình bn tự vẽ nhá :)
a, +, \(\Delta\) vuông AHC có :
AC2 = AH2 + HC2 ( Định lí py - ta - go )
202 cm = 122 cm + HC2
400 cm = 144 cm + HC2
=> HC2 = 256
HC = 16 cm
Ta có : BH + HC = BC
5 + 16 = BC
=> BC = 21 cm
+, \(\Delta\) vuông AHB :
AB2 = AH2 + BH2
AB2 = 122 cm + 52 cm
AB2 = 144 cm + 25 cm
AB2 = 169
AB = 13 cm
=> Chu vi \(\Delta\) ABC : 20 + 13 + 21 = 54
b, Diện tích \(\Delta\) ABC :
\(\frac{1}{2}.21.12=126\) ( cm2 )

















