Cho (O) đường kính AB, dây AC không đi qua tâm, H là trđ AC. tiếp tuyến tại C của (O) cắt OH tại M. Kẻ CK vuông góc với AB. I là trđ CK. c/m M,I,B thẳng hàng.

Những câu hỏi liên quan
Cho (O,R) đường kính AB, dây AC không đi qua tâm. Gọi H là trung điểm AC
a, Chứng minh OH//BC
b,Tiếp tuyến tại C (O) cắt OH tại M. Chứng minh MA là tiếp tuyến của đường tròn tâm O
c, Vẽ CK vuông góc với AB tại K. GỌi I là trung điểm của CK, đặt góc BAC = góc anfa. Chứng minh IK=R.sin anfa. cos anfa
d, Chứng minh 3 điểm M,I,B thẳng hàng
Ai giúp mình ý d vs ạ !
Cho đường tròn (O, R) đường kính AB và dây AC không qua tâm O. Gọi H là trung điểm của ACa, Tính số đo góc
A
C
B
^
và chứng minh OH//BCb, Tiếp tuyên tại C của (O) cắt OH ở M. Chứng minh đường thẳng AM là tiếp tuyến của (O) tại Ac, Vẽ CK vuông góc AB tại K. Gọi I là trung điểm của CK và đặt
C
A
B...
Đọc tiếp
Cho đường tròn (O, R) đường kính AB và dây AC không qua tâm O. Gọi H là trung điểm của AC
a, Tính số đo góc A C B ^ và chứng minh OH//BC
b, Tiếp tuyên tại C của (O) cắt OH ở M. Chứng minh đường thẳng AM là tiếp tuyến của (O) tại A
c, Vẽ CK vuông góc AB tại K. Gọi I là trung điểm của CK và đặt C A B ^ = α. Chứng minh IK = Rsinα.cosα
d, Chứng minh ba điểm M, I, B thẳng hàng
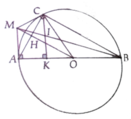
a, HS tự làm
b, HS tự làm
c, IK = 1 2 CK = 1 2 AC.sinα = R.cosα.sinα
d, Giả sử BI cắt AM tại N. Vì IK//AM => MO = OP
=> 1 O I 2 = 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => M ≡ N
Đúng 0
Bình luận (0)
Cho đường tròn (O,R) đường kính AB và dây AC không đi qua tâm. Kẻ OH vuông góc với AC tại H
a, Tính góc ACB và chứng minh OH // BC
b, Tiếp tuyến của đường tròn (O) tại C cắt OH tại M. Chứng minh: MA là tiếp tuyến của đường tròn (O)
c, BM cắt CK tại Ichứng minh: Ilà trung điểm của CK
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CA⊥CB
mà CA⊥OH
nên OH//BC
b: Xét (O) có
OH là một phần đường kính
AC là dây
OH⊥AC tại H
Do đó: H là trung điểm của AC
Xét ΔMAC có
MH là đường trung tuyến
MH là đường cao
Do đó: ΔMAC cân tại M
Xét ΔOAM và ΔOCM có
OA=OC
MA=MC
OM chung
Do đó:ΔOAM=ΔOCM
Suy ra: \(\widehat{OAM}=\widehat{OCM}=90^0\)
hay MA là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Cho(O,R) đường kính AB và dây AC không đi qua O. Gọi Hlaf trung điểm của AC a) tính góc ACB và chứng minh OH//BC b) Tiếp tuyến tại C của (O) cawts tia OH ở M. C/m: đường thẳng MA là tiếp tuyến tại A của (O) c) kẻ CK vuông góc AB tại K. Gọi I là trung điểm của CK và đặt góc CAB=α. Chứng minh Ck=2R.sinα d) Chứng minh M,I,B thẳng hàng
Cho ( O;R ) đường kính AB. Trên (O) lấy điểm C sao cho dây ACdây CB. Gọi H là trung điểm của AC. Kẻ CK vuông góc với AB tại K thuộc AB.a/ Cho AC8cm; CB5cm. CM: tam giác ACB vuông, tính CK và góc CAB ( góc làm tròn đến độ )b/ Tiếp tuyến tại C của đtr(O) cắt tia OH tại M. CM: OH//BC và MA là tiếp tuyến của (O)c/ Gọi I là trung điểm của CK. CM: IK R.sinB.cosBd/ CM: 3 điểm M,I,B thẳng hàng
Đọc tiếp
Cho ( O;R ) đường kính AB. Trên (O) lấy điểm C sao cho dây AC<dây CB. Gọi H là trung điểm của AC. Kẻ CK vuông góc với AB tại K thuộc AB.
a/ Cho AC=8cm; CB=5cm. CM: tam giác ACB vuông, tính CK và góc CAB ( góc làm tròn đến độ )
b/ Tiếp tuyến tại C của đtr(O) cắt tia OH tại M. CM: OH//BC và MA là tiếp tuyến của (O)
c/ Gọi I là trung điểm của CK. CM: IK = R.sinB.cosB
d/ CM: 3 điểm M,I,B thẳng hàng
Cho(O,R) đường kính AB và dây AC không đi qua O. Gọi Hlaf trung điểm của AC
a) tính góc ACB và chứng minh OH//BC
b) Tiếp tuyến tại C của (O) cawts tia OH ở M. C/m: đường thẳng MA là tiếp tuyến tại A của (O)
c) kẻ CK vuông góc AB tại K. Gọi I là trung điểm của CK và đặt góc CAB=α. Chứng minh Ck=2R.sinα
d) Chứng minh M,I,B thẳng hàng
Cho đường tròn(O;R),đường kính AB và dây AC không qua tâm O .Gọi H là trung điểm của AC.a)Tính góc ACB và chứng minh OH song song với BC .b)Tiếp tuyến tại C của (O) cắt OH ở M .Chứng minh đường thẳng AM lá tiếp tuyến của (O) tại A .c)Vẽ CK vuông góc với AB tại K .Gọi I là trung điểm của CK và đặt góc CABanpha.Chứng minh IK2Rsin (anpha) . cos(anpha)a)Chứng minh ba điểm M,I,B thẳng hàng.
Đọc tiếp
Cho đường tròn(O;R),đường kính AB và dây AC không qua tâm O .Gọi H là trung điểm của AC.
a)Tính góc ACB và chứng minh OH song song với BC .
b)Tiếp tuyến tại C của (O) cắt OH ở M .Chứng minh đường thẳng AM lá tiếp tuyến của (O) tại A .
c)Vẽ CK vuông góc với AB tại K .Gọi I là trung điểm của CK và đặt góc CAB=anpha.Chứng minh IK=2Rsin (anpha) . cos(anpha)
a)Chứng minh ba điểm M,I,B thẳng hàng.
Cho đường tròn (O; R), đường kính AB và dây AC không đi qua tâm. Gọi H là trung điểm AC.a)Tính số đo góc ACB và chứng minh OH // BC.b)Tiếp tuyến tại C của đường tròn ( O ) cắt tia OH tại M. Chứng minh: Đường thẳng MA là tiếp tuyến tại A của ( O )c) Vẽ CK vuông góc AB tại K. Gọi I là trung điểm của CK và đặt góc CAB α. Chứng minh: IK R. Sin α. Cos αd) Chứng minh 3 điểm M, I, B thẳng hàng
Đọc tiếp
Cho đường tròn (O; R), đường kính AB và dây AC không đi qua tâm. Gọi H là trung điểm AC.
a)Tính số đo góc ACB và chứng minh OH // BC.
b)Tiếp tuyến tại C của đường tròn ( O ) cắt tia OH tại M. Chứng minh: Đường thẳng MA là tiếp tuyến tại A của ( O )
c) Vẽ CK vuông góc AB tại K. Gọi I là trung điểm của CK và đặt góc CAB = α. Chứng minh: IK = R. Sin α. Cos α
d) Chứng minh 3 điểm M, I, B thẳng hàng
Cho đường tròn (O; R), đường kính AB và dây AC không đi qua tâm. Gọi H là trung điểm AC.a)Tính số đo góc ACB và chứng minh OH // BC.b)Tiếp tuyến tại C của đường tròn ( O ) cắt tia OH tại M. Chứng minh: Đường thẳng MA là tiếp tuyến tại A của ( O )c) Vẽ CK vuông góc AB tại K. Gọi I là trung điểm của CK và đặt góc CAB α. Chứng minh: IK R. Sin α. Cos αd) Chứng minh 3 điểm M, I, B thẳng hàng
Đọc tiếp
Cho đường tròn (O; R), đường kính AB và dây AC không đi qua tâm. Gọi H là trung điểm AC.
a)Tính số đo góc ACB và chứng minh OH // BC.
b)Tiếp tuyến tại C của đường tròn ( O ) cắt tia OH tại M. Chứng minh: Đường thẳng MA là tiếp tuyến tại A của ( O )
c) Vẽ CK vuông góc AB tại K. Gọi I là trung điểm của CK và đặt góc CAB = α. Chứng minh: IK = R. Sin α. Cos α
d) Chứng minh 3 điểm M, I, B thẳng hàng













