Tìm đẳng thức đúng:
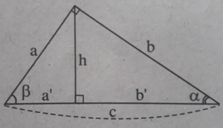
A . c o t g α = b a B . c o t g α = b c C . c o t g α = a c ' D . c o t g α = h b
Tìm đẳng thức đúng:
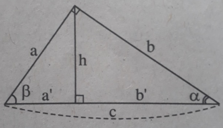
A. cotg α = 1 + tg α B. cotg α = 1 - tg α
C. cotg α = 1. tg α D. cotg α = 1/tg α
Tìm đẳng thức đúng:
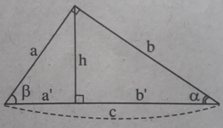
A. cos α = cos β B. cos α = tg β
C. cos α = cotg β D. cos α = sin β
Tìm đẳng thức đúng:
A. tg α = tg β B. tg α = cotg β
C. tg α = sin β D. tg α = cos β
Tìm đẳng thức đúng
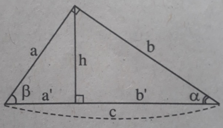
A. sin α = sin β B. sin α = cos β
C. sin α = tg β D. sin α = cotg β
Tìm đẳng thức đúng:
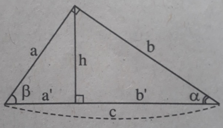
A. cotg α = tg β B. cotg α = cotg β
C. cotg α = cos β D. cotg α = sin β
Tìm đẳng thức đúng:
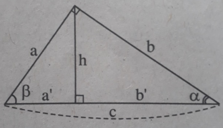
A. tg α = sin α + cos α B. tg α = sin α - cos α
C. tg α = sin α . cos α D. tgα = sin α /cos α
Trong không gian Oxyz, cho ba điểm A(0;1;2), B(2;-2;1), C(-2;0;1) và mặt phẳng α có phương trình 2 x + 2 y + z - 3 = 0 .Biết rằng tồn tại duy nhất điểm M(a;b;c) thuộc mặt phẳng α sao cho MA = MB = MC. Đẳng thức nào sau đây đúng?
A. 2 a + b - c = 0
B. 2 a + 3 b - 4 c = 41
C. 5 a + b + c = 0
D. a + 3 b + c = 0
Trong không gian Oxyz, cho ba điểm A 0 ; 1 ; 2 , B 2 ; - 2 ; 1 , C - 2 ; 0 ; 1 và mặt phẳng α có phương trình 2 x + 2 y + z - 3 = 0 . Biết rằng tồn tại duy nhất điểm M a ; b ; c thuộc mặt phẳng α sao cho M A = M B = M C . Đẳng thức nào sau đây đúng?
A. 2 a + b - c = 0
B. 2 a + 3 b - 4 c = 41
C. 5 a + b + c = 0
D. a + 3 b + c = 0
Cho 4 điểm bất kì A, B, C, O. Đẳng thức nào sau đây đúng?
A. O A → = O B → - B A →
B. O A → = C A → - C O →
C. A B → = A C → + B C →
D. A B → = O B → - O A →
Bài 1: Tính gt biểu thức: \(cos^220^o+cos^240^o+cos^250^o+cos^270^o\)
Bài 2:Chứng minh hệ thức:
a,\(cot^2\text{α}-cos^2\text{α}=cot^2\text{α}.cos^2\text{α}\)
b,\(\dfrac{1+cos\text{ α}}{sin\text{ α}}=\dfrac{sin\text{ α}}{1-cos\text{ α}}\)
(P/s: tại mik ko tìm đc kí hiệu Anpha nên phải viết chữ =.=)
Các bạn giúp mik vs, mik đang cần gấp ak.Mik cảm ơn!!!!
bài 1: ta có : \(cos^220+cos^240+cos^250+cos^270\)
\(=cos^220+cos^270+cos^240+cos^250\)
\(=cos^220+cos^2\left(90-20\right)+cos^240+cos^2\left(90-40\right)\)
\(=cos^220+sin^220+cos^240+sin^240=1+1=2\)
bài 2: a) ta có : \(cot^2\alpha-cos^2\alpha=cos^2\alpha\left(\dfrac{1}{sin^2\alpha}-1\right)=cos^2\alpha.\left(\dfrac{1-sin^2\alpha}{sin^2\alpha}\right)\)
\(=cos^2\alpha.\left(\dfrac{cos^2\alpha}{sin^2\alpha}\right)=cos^2\alpha.cot^2\alpha\left(đpcm\right)\)
b) ta có : \(sin^2\alpha+cos^2\alpha=1\Leftrightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Leftrightarrow sin^2\alpha=\left(1-cos\alpha\right)\left(1+cos\alpha\right)\Leftrightarrow\dfrac{1+cos\alpha}{sin\alpha}=\dfrac{sin\alpha}{1-cos\alpha}\left(đpcm\right)\)