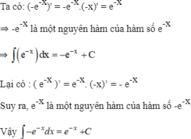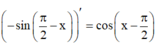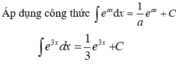Tính các nguyên hàm sau đây: ∫ x + e x e 2 x d x

Những câu hỏi liên quan
Tính các nguyên hàm sau đây: ∫ x + sin x d x cos 2 x
xtanx + ln cosx + 1 cosx + C
Hướng dẫn: Đặt u = x + sinx, dv = d(tanx)
Đúng 0
Bình luận (0)
Tính các nguyên hàm sau đây: ∫ x + sin 2 x sin x d x
sin x - x + 1 cos x + 1 3 cos 3 x + C
Hướng dẫn: Đặt u = x + sin 2 x , dv = sinxdx
Đúng 0
Bình luận (0)
Tính các nguyên hàm sau đây: ∫ x + ln x x 2 d x
x 4 4 + x 3 3 ln x - 1 3 + C
Hướng dẫn: Đặt u = x + lnx; dv = x 2 dx
Đúng 0
Bình luận (0)
Trong các cặp hàm số dưới đây, hàm số nào là nguyên hàm của hàm số còn lại? e - x v à - e - x
Trong các hàm số sau đây, hàm số nào là một nguyên hàm của
f
(
x
)
cos
π
2
-
x
Đọc tiếp
Trong các hàm số sau đây, hàm số nào là một nguyên hàm của f ( x ) = cos π 2 - x
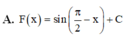
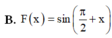
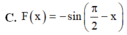
![]()
Trong các hàm số sau đây, hàm số nào là nguyên hàm của
f
(
x
)
e
3
x
A.
e
3
x
B. 3
e
3
x
C.
1
3
e
3
x
D. -3
e...
Đọc tiếp
Trong các hàm số sau đây, hàm số nào là nguyên hàm của f ( x ) = e 3 x
A. e 3 x
B. 3 e 3 x
C. 1 3 e 3 x
D. -3 e 3 x
Trong các hàm số sau đây, hàm số nào là một nguyên hàm của
f
x
cos
π
2
−
x
A.
F
x
sin
π
2...
Đọc tiếp
Trong các hàm số sau đây, hàm số nào là một nguyên hàm của f x = cos π 2 − x
A. F x = sin π 2 + x
B. F x = sin π 2 + x
C. F x = - sin π 2 − x
D. F(x) = cos x
Đáp án C
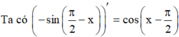
Chú ý
* Theo định nghĩa, nguyên hàm của hàm số f(x) là các hàm số F(x) thõa mãn điều kiện F ' x = f x , ∀ x ∈ K
* Để tìm họ nguyên hàm của hàm số f(x), các em chỉ cần tìm một nguyên hàm F(x) của nó
Đúng 0
Bình luận (0)
Tìm các nguyên hàm sau đây
a) \(I_1=\int e^{2x}\sin3xdx\)
b) \(I_2=\int e^{-x}\cos\frac{x}{2}dx\)
c) \(I_2=\int e^{3x}\cos\left(e^x\right)d\)
Đối với cả ba nguyên hàm đã cho, ta sẽ áp dụng liên tiếp hai làn lấy nguyên hàm từng phần và trong hai lần việc chọn hàm \(u=u\left(x\right)\) là tùy ý ( còn \(dv\) là phần còn lại của biểu thức dưới dấu nguyên hàm. Sau phép lấy nguyên hàm từng phần kép đó ta sẽ thu được một phương trình bậc nhất với ẩn là nguyên hàm cần tìm
a) Đặt \(u=e^{2x}\) ,\(dv=\sin3xdx\)
Từ đó \(du=2e^{2x}dx\) , \(v=\int\sin3xdx=-\frac{1}{3}\cos3xdx\) Do đó :
\(I_1=-\frac{1}{3}e^{2x}\cos3x+\frac{2}{3}\int e^{2x}\cos3xdx\)
\(=-\frac{1}{3}e^{2x}\cos3x+\frac{2}{3}.I'_1\)\(I'_1=\int e^{2x}\cos3xdx\)
Ta áp dụng công thức lấy nguyên hàm từng phần
Đặt \(u=e^{2x}\) ; \(dv=\cos3xdx\) Khi đó \(du=2^{2x}dx\); \(v=\frac{1}{3}\sin2x\)
Do đó \(I'_1=\frac{1}{3}e^{2x}\sin3x-\frac{2}{3}\int e^{2x}\sin3xdx\) Như vậy :
\(I_1=-\frac{1}{3}e^{2x}\cos3x+\frac{2}{9}e^{2x}\sin3x-\frac{4}{9}\int e^{2x}\sin3xdx\)
\(I_1=\int e^{2x}\sin3xdx\)
Tức là \(I_1=-\frac{1}{3}e^{2x}\cos3x+\frac{2}{9}\sin3x-\frac{4}{9}I_1\)
Ta có \(I_1=\frac{3}{13}e^{2x}\left(\frac{2}{3}\sin3x-\cos3x\right)+C\)
Đúng 0
Bình luận (0)
b) Đặt \(u=e^{-x}\) ; \(dv=\cos\frac{x}{2}dx\)
Từ đó :
\(du=-e^{-x}dx\) ; \(v=\int\cos\frac{x}{2}dx=2\int\cos\frac{x}{2}d\left(\frac{x}{2}\right)=2\sin\frac{x}{2}\)
Do đó :
\(I_2=2e^{-x}\sin\frac{x}{2}+2\int e^{-x}\sin\frac{x}{2}dx\) (b)
\(\int e^{-x}\sin\frac{x}{2}dx=I'_2\)
Ta cần tính \(I'_2\) Đặt \(u=e^{-x}\) ; \(dv=\sin\frac{x}{2}dx\)
Từ đó :
\(du=-e^{-x}dx\) ; \(v=\int\sin\frac{x}{2}dx=-2\cos\frac{x}{2}\)
Do đó :
\(I'_2=-2e^{-x}\cos\frac{x}{2}-2\int e^{-x}\cos\frac{x}{2}dx\)
\(=-2e^{-x}\cos\frac{x}{2}-2I_2\)
Thế \(I'_2\) vào (b) ta thu được phương trình bậc nhất với ẩn là \(I_2\)
\(I_2=2e^{-x}\sin\frac{x}{2}+2\left[-2e^{-x}\cos\frac{x}{2}-2I_2\right]\)
hay là
\(5I_2=2e^{-x}\sin\frac{x}{2}-4e^{-x}\cos\frac{x}{2}\) \(\Rightarrow\) \(I_2=\frac{2}{5}e^{-x}\left(\sin\frac{x}{2}-2\cos\frac{x}{2}\right)+C\)
Đúng 0
Bình luận (0)
c) Trước khi áp dụng công thức lấy nguyên hàm từng phần ta thực hiện phép đổi biến \(t=e^x\).
Khi đó : \(I_2=\int t^2\cos tdt=t^2\sin t-2\int t\sin tdt\)
\(=t^2\sin t-2\left(-t\cos t+\int\cos tdt\right)\)
=\(\left(t^2-2\right)\sin t+2t\cos t+C\)
\(=\left(e^{2x}-2\right)\sin e^x+2e^x\cos e^x+C\)
Đúng 0
Bình luận (0)
Hàm số nào trong các hàm số sau đây là một nguyên hàm của hàm số
y
e
-
2
x
A.
y
-
e
-
2
x
2
B.
y
-
2
e
-
2
x...
Đọc tiếp
Hàm số nào trong các hàm số sau đây là một nguyên hàm của hàm số y = e - 2 x
A. y = - e - 2 x 2
B. y = - 2 e - 2 x + C ( C ∈ R )
C. y = 2 e - 2 x + C ( C ∈ R )
D. y = e - 2 x 2