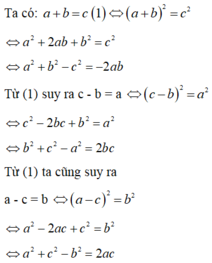cho a2-b2-c2=0. hãy tìm kết quả của (-3b+4c+5a)

Những câu hỏi liên quan
cho a2-b2-c2=0. hãy tìm kết quả của (-3b+4c+5a)
mình đang thi giúp mình với
Cho A2=80, B2=130, C2=180. Em hãy điền kết quả TRUE, FALSE cho các câu sau đây?
a. =OR(A2>B2,B2>C2) Kết quả: ......................
b. =OR(B2-A2>40,C2>B2+40) Kết quả: ......................
c. =AND(A2>B2,C2-A2>B2) Kết quả: ......................
d. =AND(A2*B2<A2*C2) Kết quả: ......................
câu 3: Trong ô A2 của trang tỉnh có số 4.32, ô B2 có số 7.65. Nếu trong ở C2 có công thức =SUM(A2,B2). Hãy cho kết quả của ô C2 trong mỗi trưởng hợp sau:
a Số trong ô C2 được định dạng có2 chữ số thập phẩn
b/ Số trong ở C2 được định dạng có 1 chữ số thập phẩn
c/ Số trong ô C2 được định dạng là số nguyên
Các số thực a,b,c,x,y,z thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
c
+
4
0
và
x
2
+
y
2
+
z
2
-
4
x
+
4
y
+
4...
Đọc tiếp
Các số thực a,b,c,x,y,z thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 c + 4 = 0 và x 2 + y 2 + z 2 - 4 x + 4 y + 4 = 0 . Tìm GTLN của S = a - x 2 + b - y 2 + z - c 2 .
![]()
![]()
![]()
![]()
cho a+b+c=0 và a≠0,b≠0,c≠0 tính M
M=a2/a2-b2-c2 +b2/b2-c2-a2 +c2/c2-a2-b2
Ta có: a+b+c=0
nên a+b=-c
Ta có: \(a^2-b^2-c^2\)
\(=a^2-\left(b^2+c^2\right)\)
\(=a^2-\left[\left(b+c\right)^2-2bc\right]\)
\(=a^2-\left(b+c\right)^2+2bc\)
\(=\left(a-b-c\right)\left(a+b+c\right)+2bc\)
\(=2bc\)
Ta có: \(b^2-c^2-a^2\)
\(=b^2-\left(c^2+a^2\right)\)
\(=b^2-\left[\left(c+a\right)^2-2ca\right]\)
\(=b^2-\left(c+a\right)^2+2ca\)
\(=\left(b-c-a\right)\left(b+c+a\right)+2ca\)
\(=2ac\)
Ta có: \(c^2-a^2-b^2\)
\(=c^2-\left(a^2+b^2\right)\)
\(=c^2-\left[\left(a+b\right)^2-2ab\right]\)
\(=c^2-\left(a+b\right)^2+2ab\)
\(=\left(c-a-b\right)\left(c+a+b\right)+2ab\)
\(=2ab\)
Ta có: \(M=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)
\(=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
\(=\dfrac{a^3+b^3+c^3}{2abc}\)
Ta có: \(a^3+b^3+c^3\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ca-cb+c^2\right)-3ab\left(a+b\right)\)
\(=-3ab\left(a+b\right)\)
Thay \(a^3+b^3+c^3=-3ab\left(a+b\right)\) vào biểu thức \(=\dfrac{a^3+b^3+c^3}{2abc}\), ta được:
\(M=\dfrac{-3ab\left(a+b\right)}{2abc}=\dfrac{-3\left(a+b\right)}{2c}\)
\(=\dfrac{-3\cdot\left(-c\right)}{2c}=\dfrac{3c}{2c}=\dfrac{3}{2}\)
Vậy: \(M=\dfrac{3}{2}\)
Đúng 2
Bình luận (0)
Cho abc ≠ 0; a + b c. Tính giá trị của biểu thức
B
(a
2
+
b
2
−
c
2
)(b
2
+
c
2
−
a
2...
Đọc tiếp
Cho abc ≠ 0; a + b = c. Tính giá trị của biểu thức B = (a 2 + b 2 − c 2 )(b 2 + c 2 − a 2 )(c 2 + a 2 − b 2 ) 8a 2 b 2 c 2
A. -1
B. 1
C. 2
D. -2
tìm a,b,c biết 4a-b2=4b-c2=4c-a2=1
Câu 1. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 2. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Câu 3. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Hãy giải ba câu hỏi này
Bài 2:
Ta có: M = a2+ab+b2 -3a-3b-3a-3b +2001
=> 2M = ( a2 + 2ab + b2) -4.(a+b) +4 + (a2 -2a+1)+(b2 -2b+1) + 3996
2M= ( a+b-2)2 + (a-1)2 +(b-1)2 + 3996
=> MinM = 1998 tại a=b=1
Câu 3:
Ta có: P= x2 +xy+y2 -3.(x+y) + 3
=> 2P = ( x2 + 2xy +y2) -4.(x+y) + 4 + (x2 -2x+1) +(y2 -2y+1)
2P = ( x+y-2)2 +(x-1)2+(y-1)2
=> MinP = 0 tại x=y=1
Bài1:
Ta có: a2+ b2+c2+d2= a.(b+c+d)
=> a2+b2+c2+d2 -ab -ac -ad =0
=> 4a2+ 4b2+4c2+4d2-4ab -4ac -4ad=0
=> ( a2 - 4ab +4b2) + ( a2- 4ac + 4c2) +( a2 -4ad+ 4d2) + a2=0
=> ( a-2b)2 + ( a-2c)2 + (a-2d)2 + a2 =0
=> ....
KL: a=b=c=d=0
cho a,b,c khác 0 ; a+b+c=0 tính a=1/(a2+b2-c2)+1/(b2+c2-a2)+1/(a2+c2-b2)
Câu hỏi của Hattory Heiji - Toán lớp 8 - Học toán với OnlineMath
tvbobnokb' n
iai
ni;bv nn0