câu 2 : 

a) có phải là chứng minh AM ⊥ BC không

xét ΔAMB và ΔAMC, ta có : 

AB = AC (2 cạnh bên của ΔABC cân tại A)

MB = MC (AM là đường trung tuyến của cạnh BC)

AM là cạnh chung

=> ΔAMB = ΔAMC (c.c.c)

=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)

mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)

\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)

=> AM ⊥ BC

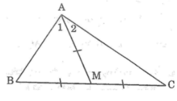
Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC

Mà AM = 1/2 BC (gt) nên: AM = BM = MC.

Tam giác AMB có AM = MB nên ΔAMB cân tại M

Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)

Tam giác AMC có AM = MC nên ΔAMC cân tại M

Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)

Trong ΔABC ta có:

∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)

Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180o ⇔ 2∠(BAC) = 180o

Hay ∠(BAC) = 90o.

Vậy ΔABC vuông tại A.

ΔABC vuông tại A có AM là trung tuyến

nên MA=MB

mà MA=AB

nên MA=AB=MB

=>ΔMAB đều

=>góc B=60 độ

=>góc C=90-60=30 độ

sin C=sin 30=1/2

a: Xét ΔABM và ΔACM có

AB=AC
AM chung

BM=CM

Do đó: ΔABM=ΔACM

b: Ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường cao

c: BM=CM=BC/2=8(cm)

nên AM=6(cm)

tham khảo

a: Xét ΔABM và ΔACM có

AB=AC
AM chung

BM=CM

Do đó: ΔABM=ΔACM

b: Ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường cao

c: BM=CM=BC/2=8(cm)

nên AM=6(cm)

a, Ta có :

AB = AC (gt)

=> Δ ABC cân tại A

Xét Δ ABM và Δ ACM, có :

AB = AC (gt)

MB = MC (M là trung điểm BC)

\(\widehat{ABM}=\widehat{ACM}\) (Δ ABC cân tại A)

=> Δ ABM = Δ ACM

b, Ta có :

AM là đường trung tuyến

Δ ABC cân tại A

=> AM ⊥ BC

c, Ta có :

BC = 2MB

=> 16 = 2MB

=> MB = 8 (cm)

Xét Δ AMB vuông tại M, có :

\(AB^2=AM^2+BM^2\)

=> \(10^2=AM^2+8^2\)

=> \(AM^2=36\)

=> AM = 6 (cm)