Tập xác định của hàm số f ( x ) = - x 2 + 2 x x 2 + 1 là tập hợp nào sau đây?
A. R \ - 1 ; 1
B.R
C. R \ 1
D. R \ - 1
Những câu hỏi liên quan
Cho hàm số y=f(x) xác định bởi công thức: \(y=\frac{-18}{\left|2x-1\right|}\)
a) Tìm đk xác định và tập xác định của hàm số.
b) Biết \(x\in\left\{-4;-2;-1;0;1;2;3\right\}\). Hãy viết tập hợp các cặp số xác định bởi hàm số y=f(x)
Câu a mình làm đc r, nhờ m.n làm hộ mình câu b và ý nhỏ này nx nhé, cũng nằm trong bài.
c) Tìm \(x\in Z\) để hàm số y=f(x) đạt GTNN? Tính giá trị đó.
Tập xác định của hàm số
f
(
x
)
(
x
-
3
)
1
3
là
A
.
[
3
;
+
∞
)
B
.
(
3
;
+
∞
)
C...
Đọc tiếp
Tập xác định của hàm số f ( x ) = ( x - 3 ) 1 3 là
A . [ 3 ; + ∞ )
B . ( 3 ; + ∞ )
C . ℝ \ { 3 }
D . ℝ
Chọn B
Hàm số là hàm lũy thừa với số mũ không nguyên.
Điều kiện xác định: 
. Vậy tập xác định của hàm số đã cho là 
.
Đúng 0
Bình luận (0)
Tập xác định của hàm số
f
(
x
)
(
x
-
3
)
1
3
là A.
[
3
;
+
∞
)
B.
(
3
;
+
∞
)
C. R {3} D. R
Đọc tiếp
Tập xác định của hàm số f ( x ) = ( x - 3 ) 1 3 là
A. [ 3 ; + ∞ )
B. ( 3 ; + ∞ )
C. R \ {3}
D. R
Tập xác định của hàm số
f
(
x
)
1
1
-
cos
x
là:
Đọc tiếp
Tập xác định của hàm số f ( x ) = 1 1 - cos x là:
Hình dưới đây là đồ thị của hàm số y=f’(x)
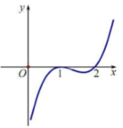
Tập xác định của hàm số là?
A. (2;+∞)
B. (0;1)
C. (1;2)
D. (-∞;1)
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Đúng 0
Bình luận (0)
Tập xác định của hàm số
y
f
(
x
)
x
-
3
-
4
-
x
là: A. [3; 4] B. R (3; 4) C. (3; 4) D. R [3; 4].
Đọc tiếp
Tập xác định của hàm số y = f ( x ) = x - 3 - 4 - x là:
A. [3; 4]
B. R \ (3; 4)
C. (3; 4)
D. R \ [3; 4].
Tập xác định của hàm số f(x)
-
x
2
+
2
x
x
2
+
1
là tập hợp nào sau đây? A.
ℝ
{-1;1} B.
ℝ
C.
ℝ
1} D.
ℝ
{-1}
Đọc tiếp
Tập xác định của hàm số f(x) = - x 2 + 2 x x 2 + 1 là tập hợp nào sau đây?
A. ℝ \{-1;1}
B. ℝ
C. ℝ \1}
D. ℝ \{-1}
Chọn B
Phương pháp:
Sử dụng phân thức có nghĩa khi mẫu thức khác 0 để tìm xác định của hàm số.
Cách giải:
Điều kiện: 
Suy ra tập xác định D = ℝ .
Đúng 0
Bình luận (0)
Tìm tập xác định D của hàm số
f
(
x
)
(
4
x
-
3
)
1
2
. A. D R
{
4
3
}
B. D R C. D
[
3
4
;
...
Đọc tiếp
Tìm tập xác định D của hàm số f ( x ) = ( 4 x - 3 ) 1 2 .
A. D = R \ { 4 3 }
B. D = R
C. D = [ 3 4 ; + ∞ )
C. D = ( 3 4 ; + ∞ )
