Cho hình chóp đều S . A B C có góc giữa mặt bên và mặt phẳng đáy A B C bằng 60 0 , khoảng cách giữa hai đường thẳng S A và B C bằng 6 7 7 . Thể tích của khối chóp S . A B C bằng
A. V = 8 3 3 .
B. V = 5 7 3 .
C. V = 10 7 3 .
D. V = 5 3 2 .
Những câu hỏi liên quan
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝Tan của góc giữa mặt bên và mặt đáy bằng: A.
tan
α
B.
c
o
t
α
C.
2
tan
α
D.
2
2
tan
α
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
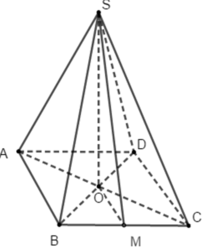
Tan của góc giữa mặt bên và mặt đáy bằng:
A. tan α
B. c o t α
C. 2 tan α
D. 2 2 tan α
Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)
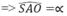
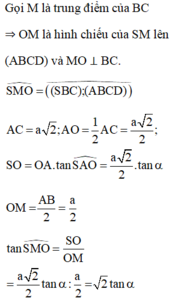
Đáp án C
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:10
Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b.
a) Tính sin của góc tạo bởi cạnh bên và mặt đáy.
b) Tính tang của góc giữa mặt phẳng chứa mặt đáy và mặt phẳng chứa mặt bên.
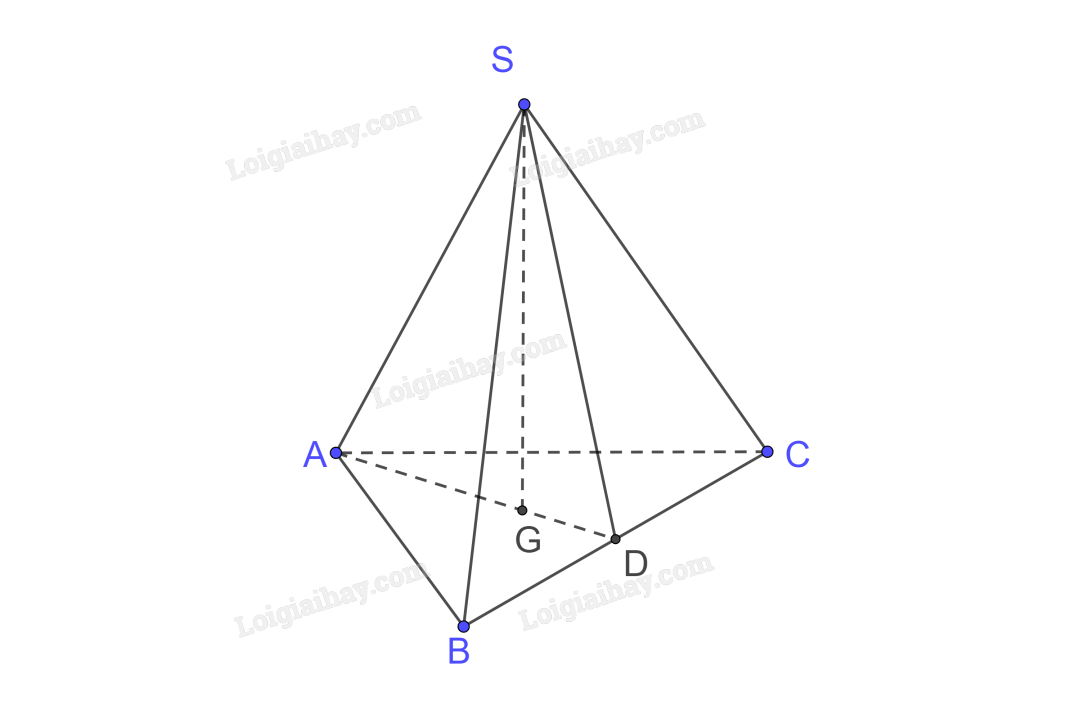
Vì hình chóp S.ABC đều, gọi G là hình chiếu của S trên (ABC) nên G là tâm của đáy ABC là tam giác đều do đó G cũng là trọng tâm hay trực tâm của tam giác ABC.
Gọi AG cắt BC tại D
a) Ta có A là hình chiếu của A trên (ABC)
G là hình chiếu của S trên (ABC)
\( \Rightarrow \) AG là hình chiếu của SA trên (ABC)
\( \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,AG} \right) = \widehat {SAG}\)
Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Mà G là trọng tâm nên \(AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)
Xét tam giác SAG vuông tại G có
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
\(\sin \widehat {SAG} = \frac{{SG}}{{SA}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :b = \sqrt {1 - \frac{{{a^2}}}{{3{b^2}}}} \)
b) Ta có \(AG \bot BC,SG \bot BC \Rightarrow BC \bot \left( {SAD} \right);SD \subset \left( {SAD} \right) \Rightarrow BC \bot SD\)
\(BC \bot AD\) (G là trực tâm)
\(\begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\ \Rightarrow \left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {AD,SD} \right) = \widehat {SDA}\end{array}\)
Mà G là trọng tâm nên \(GD = \frac{1}{3}AD = \frac{{a\sqrt 3 }}{6}\)
Xét tam giác SGD vuông tại G có
\(\tan \widehat {SGD} = \frac{{SG}}{{GD}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :\frac{{a\sqrt 3 }}{6} = \frac{6}{{a\sqrt 3 }}.\sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
Đúng 0
Bình luận (0)
Cho hình chóp đều S.ABCD, cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là
60
o
. Tính khoảng cách từ điểm B đến mặt phẳng (SCD).
Đọc tiếp
Cho hình chóp đều S.ABCD, cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là 60 o . Tính khoảng cách từ điểm B đến mặt phẳng (SCD).
Cho hình chóp đều S.ABCD, cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là
60
0
. Tính khoảng cách từ điểm B đến mặt phẳng
S
C
D
. A.
a
4
B.
a
3
4
C.
a
3
2...
Đọc tiếp
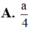
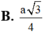
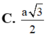
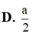
Cho hình chóp đều S.ABCD, cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là 60 0 . Tính khoảng cách từ điểm B đến mặt phẳng S C D .
A. a 4
B. a 3 4
C. a 3 2
D. a 2
Cho hình chóp đều S.ABCD, cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là
60
°
. Tính khoảng cách từ điểm B đến mặt phẳng (SCD). A.
a
4
B.
a
3
4
C.
a
3
2
D.
a
2
Đọc tiếp
Cho hình chóp đều S.ABCD, cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là 60 ° . Tính khoảng cách từ điểm B đến mặt phẳng (SCD).
A. a 4
B. a 3 4
C. a 3 2
D. a 2
Đáp án là C.
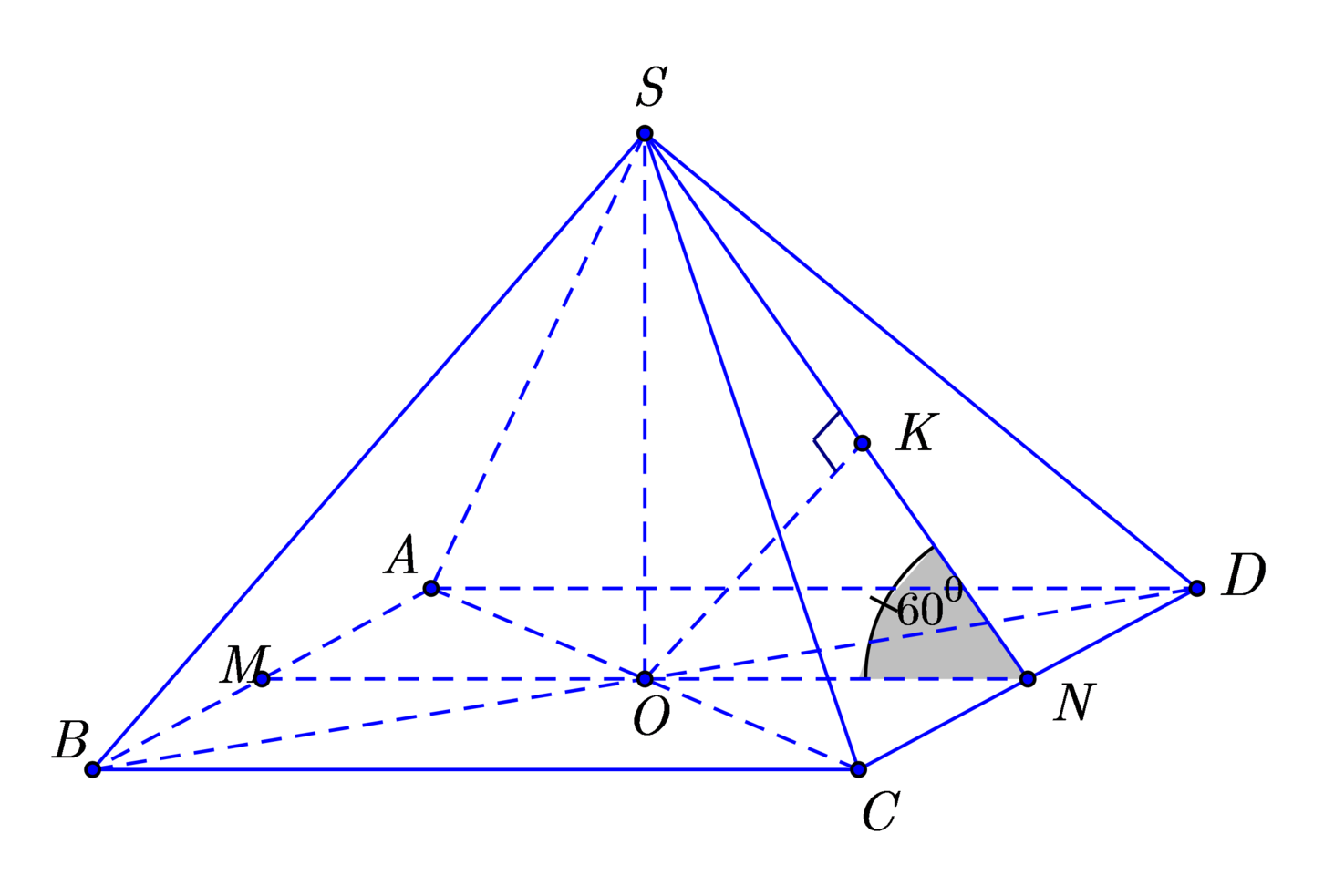
+ S C D ; A B C D ^ = S N O ^ = 60 0 .
+ A B / / C D ⇒ A B / / S C D
⇒ d B ; S C D = d M ; S C D ; (M là trung điểm AB).
S O = O N . tan 60 0 = a 3 2 ; 1 O K 2 = 1 O S 2 + 1 O N 2 = 16 3 a 2 ⇒ O K = d O ; S C D = a 3 4
+ d M ; S C D = 2 d O ; S C D = 2 O K = a 3 2 .
Đúng 0
Bình luận (0)
Câu 1. Cho hình chóp S ABC . có SA vuông góc với ABC và đáy ABC đều cạnh a. Biết SA3a/2.Gọi H là trung điểm của BC.a. Tính góc giữa hai mặt phẳng SBC và ABC ?b. Tính diện tích của tam giác ABC từ đó suy ra diện tích tam giác SBC ?c. Chứng minh SBC vuông góc với SAH Câu 2. Cho hình chóp tam giác đều S ABC . có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi mặt bên và mặt đáy
Đọc tiếp
Câu 1. Cho hình chóp S ABC . có SA vuông góc với ABC và đáy ABC đều cạnh a. Biết SA=3a/2.Gọi H là trung điểm của BC.
a. Tính góc giữa hai mặt phẳng SBC và ABC ?
b. Tính diện tích của tam giác ABC từ đó suy ra diện tích tam giác SBC ?
c. Chứng minh SBC vuông góc với SAH
Câu 2. Cho hình chóp tam giác đều S ABC . có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi mặt bên và mặt đáy
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, mặt bên (SBC) là tam giác đều và nằm trong mặt phẳng vuông góc đáy (tham khảo hình vẽ bên). Tang góc giữa đường thẳng SA và mặt phẳng (ABC) bằng A.
3
B.
6
3
C.
6
2
D.
3
3
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, mặt bên (SBC) là tam giác đều và nằm trong mặt phẳng vuông góc đáy (tham khảo hình vẽ bên). Tang góc giữa đường thẳng SA và mặt phẳng (ABC) bằng
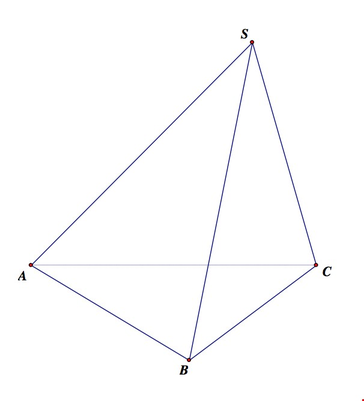
A. 3
B. 6 3
C. 6 2
D. 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng
60
0
. Tính thể tích V của khối chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng 60 0 . Tính thể tích V của khối chóp S.ABCD.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng
60
°
. Tính thể tích V của khối chóp S.ABCD. A.
V
a
3
15
6
B.
V
a
3...
Đọc tiếp
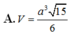
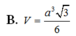
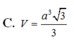
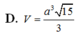
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng 60 ° . Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 15 6
B. V = a 3 3 6
C. V = a 3 3 3
D. V = a 3 15 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) là tam giác cân tại đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy là 60o. Tính thể tích khối chóp S.ABCD A.
a
3
5
B.
a
3
5
3
C....
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) là tam giác cân tại đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy là 60o. Tính thể tích khối chóp S.ABCD
A. a 3 5
B. a 3 5 3
C. a 3 3 6
D. a 3 15 6
Đáp án D
Gọi H là trung điểm của AD, khi đó từ giả thiết ta có SH ⊥ (ABCD). Ta có:
Đúng 0
Bình luận (0)