Gọi diện tích hình phẳng giới hạn bởi P : y = x 2 , tiếp tuyến tại A(1;1) và trục Oy bằng S 1 . Diện tích hình phẳng giới hạn bởi P : y = x 2 , tiếp tuyến tại A(1;1) và trục Ox bằng S 2 . Khi đó S 1 S 2 bằng
A. 1 4
B. 4
C. 1 3
D. 3
Gọi diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 tiếp tuyến tại A(1;1) và trục Oy bằng S 1 . Diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 tiếp tuyến tại A(1;1) và trục Ox bằng S 2 . Khi đó, tỉ số S 1 S 2 bằng:
A. 1/4
B. 3
C. 1/3
D. 4
Gọi diện tích hình phẳng giới hạn bởi (P): y = x 2 tiếp tuyến tại A(1;1) và trục Oy bằng S 1 Diện tích hình phẳng giới hạn bởi (P) tiếp tuyến tại A và trục Ox bằng S 2 Khi đó, tỉ số S 1 S 2 bằng:
A. 1/4
B. 4.
C. 1/3
D. 3.
Gọi diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 , tiếp tuyến tại A(1;1) và trục Oy bằng S 1 . Diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 , tiếp tuyến tại A(1;1) và trục Ox bằng ( S 2 ) . Khi đó S 1 S 2 bằng
A. 1/4
B. 4
C. 1/3
D. 3
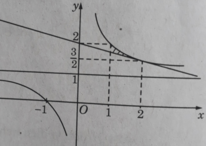
Tính diện tích của hình phẳng giới hạn bởi các đường sau: y = 1 x + 1 ,x=1 và tiếp tuyến với đường y = 1 x + 1 tại điểm (2; 3/2)
Miền cần tính diện tích được thể hiện trên Hình 10:
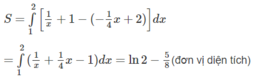
(vì tiếp tuyến với đồ thị của 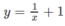
tại điểm (2;3/2) có phương trình là
![]()
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = x 3 – 1 và tiếp tuyến với y = x 3 – 1 tại điểm (-1; -2).
Đáp số: 27/4
Hướng dẫn: Phương trình tiếp tuyến tại (-1; -2) là y = 3x + 1. Do đó, diện tích :
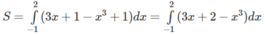
Diện tích hình phẳng giới hạn bởi P : y = x 2 + 3 , tiếp tuyến của (P) tại điểm có hoành độ x = 2 và trục tung bằng
A. 8 3
B. 4 3
C. 2
D. 7 3
Chọn A
PTTT của (P) tại x = 2 là y = 4x + 3
Xét pt
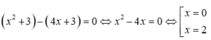
Suy ra
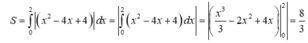
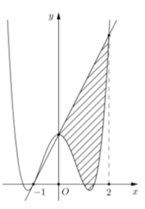
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5
Đáp án D
y ' = 4 a x 3 + 2 b x , y ' 1 = - 4 a - 2 b
Phương trình tiếp tuyến tại A là: d: y=(-4a-2b)(x+1)
Xét phương trình tương giao: a x 4 + b x 2 + c = ( - 4 a - 2 b ) ( x + 1 )
Phương trình có 2 nghiệm x=0,x=2 => 4 a + 2 b + c = 0 28 a + 10 b + c = 0 ( 1 )
∫ 0 2 - 4 a - 2 b x + 1 - a x 4 - b x 2 - c d x = - 2 a - b x 2 + - 4 a - 2 b x - a x 5 5 - b x 3 3 - c x 2 0 = - 112 5 a - 32 3 b - 2 c = 28 5 2 1 , 2 ⇒ a = 1 b = - 3 ⇒ y = x 4 - 3 x 2 + 2 , d : y = 2 x + 2 c = 2 ⇒ S = ∫ - 1 0 x 4 - 3 x 2 + 2 d x = x 5 5 - x 3 - x 2 0 - 1 = 1 5
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = − 1 ; x = 0 có diện tích bằng:

A. 2 5 .
B. 1 9 .
C. 2 9 .
D. 1 5 .
Đáp án D

∫ 0 2 [ ( − 4 a − 2 b ) ( x + 1 ) − ax 4 − b x 2 − c ] d x = [ ( − 2 a − b ) x 2 + ( − 4 a − 2 b ) x − ax 5 5 − b x 3 3 − c x ] 2 0 = − 112 5 a − 32 3 b − 2 c = 28 5 ( 2 ) ( 1 ) , ( 2 ) ⇒ a = 1 b = − 3 c = 2 ⇒ y = x 4 − 3 x 2 + 2 , d : y = 2 x + 2 ⇒ S = ∫ − 1 0 ( x 4 − 3 x 2 + 2 ) d x = x 5 5 − x 3 − x 2 0 − 1 = 1 5