Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Gọi diện tích hình phẳng giới hạn bởi
(
P
)
:
y
x
2
tiếp tuyến tại A(1;1) và trục Oy bằng
S
1
. Diện tích hình phẳng giới hạn bởi
(
P
)
:
y
x
2
tiếp tuyến tại A(1;1) và trục Ox bằng
S
2
. Khi đó, tỉ số...
Đọc tiếp
Gọi diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 tiếp tuyến tại A(1;1) và trục Oy bằng S 1 . Diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 tiếp tuyến tại A(1;1) và trục Ox bằng S 2 . Khi đó, tỉ số S 1 S 2 bằng:
A. 1/4
B. 3
C. 1/3
D. 4
Gọi diện tích hình phẳng giới hạn bởi
P
:
y
x
2
, tiếp tuyến tại A(1;1) và trục Oy bằng
S
1
. Diện tích hình phẳng giới hạn bởi
P
:
y
x
2
, tiếp tuyến tại A(1;1) và trục Ox bằng
S
2
. Khi đó
S...
Đọc tiếp
Gọi diện tích hình phẳng giới hạn bởi P : y = x 2 , tiếp tuyến tại A(1;1) và trục Oy bằng S 1 . Diện tích hình phẳng giới hạn bởi P : y = x 2 , tiếp tuyến tại A(1;1) và trục Ox bằng S 2 . Khi đó S 1 S 2 bằng
A. 1 4
B. 4
C. 1 3
D. 3
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Diện tích S của hình phẳng giới hạn bởi parabol
(
P
)
:
y
x
2
-
1
,
tiếp tuyến của (P) tại M(0;1) và trục Oy là: A. S 1.
B
.
S
...
Đọc tiếp
Diện tích S của hình phẳng giới hạn bởi parabol ( P ) : y = x 2 - 1 , tiếp tuyến của (P) tại M(0;1) và trục Oy là:
A. S = 1.
B . S = 1 4 .
C . S = 1 3 .
D . S = 7 3 .
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
f
x
, trục hoành, đường thẳng x a, x b( như hình bên). Biết
∫
a
c
f
x
d
x
−
2
v
à
∫
c
b
f
x
d
x
5
. Hỏi S bằng ba...
Đọc tiếp
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f x , trục hoành, đường thẳng x = a, x = b( như hình bên). Biết ∫ a c f x d x = − 2 v à ∫ c b f x d x = 5 . Hỏi S bằng bao nhiêu?
A. 7
B. 5
C. 2
D. 3
Tính diện tích hình phẳng giới hạn bởi đường cong
y
x
2
, tiếp tuyến với đường cong đó tại điểm có hoành độ bằng 2 và trục Oy. A.
−
40
3
B.
8
3
C.
20
3
D.
68
3
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi đường cong y = x 2 , tiếp tuyến với đường cong đó tại điểm có hoành độ bằng 2 và trục Oy.
A. − 40 3
B. 8 3
C. 20 3
D. 68 3
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
+
1
x
-
2
và các trục tọa độ Ox, Oy ta được: S
a
ln
b
c
-
1
. Biết a nguyên dương . Chọn đáp án đúng A . a + b + c 8 B . a b C . a – b + c 1 D . a + 2b – 9 c
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm
số y = x + 1 x - 2 và các trục tọa độ Ox, Oy ta được: S=
a ln b c - 1 . Biết a nguyên dương . Chọn đáp án đúng
A . a + b + c = 8
B . a > b
C . a – b + c = 1
D . a + 2b – 9 = c
Cho hình phẳng (H) giới hạn bởi đường cong (C): y = e x , tiếp tuyến của (C) tại điểm M(1;e) và trục Oy. Diện tích của (H) bằng
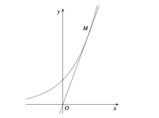
A. (e+2)/2.
B. (e-1)/2.
C. (e+1)/2.
D. (e-2)/2.
Tính diện tích S hình phẳng giới hạn bởi các đường y = x 2 + 1 , x = - 1 , x = 2 và trục hoành
A. S=6
B. S=13/6
C. S=13
D. S=16




