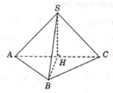
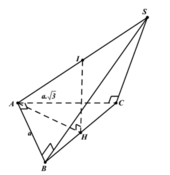
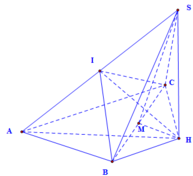
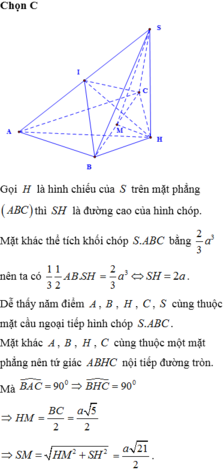
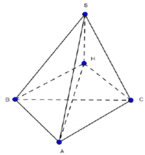
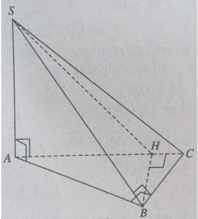
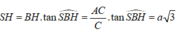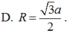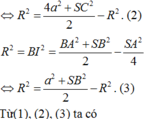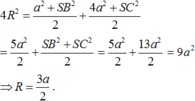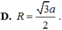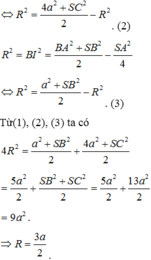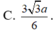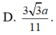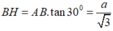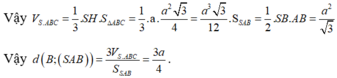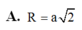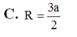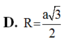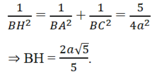Cho hình chóp S . A B C có đáy A B C là tam giác vuông tại B , A B = a , B C = a 3 . Hình chiếu vuông góc của S trên mặt đáy là trung điểm của cạnh A C .Biết S B = a 2 . Tính theo a khoảng cách từ H đến mặt phẳng S A B
A. 7 a 21 3
B. a 21 7
C. a 21 3
D. 3 a 21 7