Chứng tỏ rằng với mọi số thực z, ta luôn phần thực và phần ảo của nó không vượt quá mô đun của nó.

Những câu hỏi liên quan
Chứng tỏ rằng với mọi số phức \(z\), ta luôn có phần thực và phần ảo của \(z\) không vượt qua môđun của nó ?
Giả sử z = a + bi
Khi đó: |z|=√a2+b2|z|=a2+b2
Từ đó suy ra:
|z|=√a2=|a|≥a,|z|=√b2=|b|≥b
Đúng 0
Bình luận (0)
Hãy biểu diễn các số phức z trên mặt phẳng tọa độ, biết |z| ≤ 2 và:
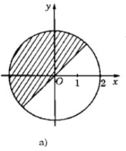
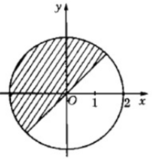
a) Phần thực của z không vượt quá phần ảo của nó;
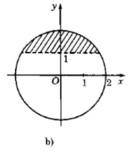
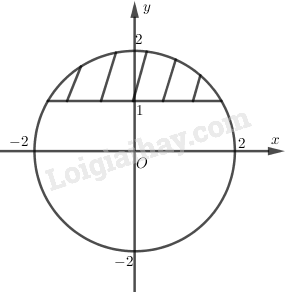
b) Phần ảo của z lớn hơn 1;
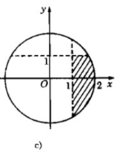
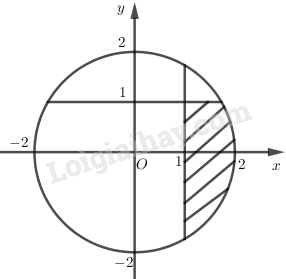
c) Phần ảo của z nhỏ hơn 1, phần thực của z lớn hơn 1.
Hãy biểu diễn các số phức z trên mặt phẳng tọa độ, biết |z| ≤ 2 và: Phần thực của z không vượt quá phần ảo của nó
Thế nào là phần thực phần ảo, mô đun của một số phức? Viết công thức tính mô đun của số phức theo phần thực phần ảo của nó?
Mỗi số phức là một biểu thức z = a + bi với a, b ∈ R, i 2 = -1
- Số thực a là phần thực của số phức: z = a + bi
- Số thực b là phần ảo của số phức z = a + bi
- Môđun của số phức z = a + bi là 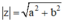
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bằng phần ảo của nó ;
b) Phần thực của z là số đối của phần ảo của nó ;
c) Phần ảo của z bằng hai lần phần thực của nó cộng với 1;
d) Modun của z bằng 1, phần thực của z không âm.
a) Đường phân giác của góc phần tư thứ nhất và góc pần tư thứ ba.
b) Đường phân giác của góc phần tư thứ hai và góc phần tư thứ tư.
c) Đường thẳng y = 2x + 1
d) Nửa đường tròn tâm O bán kính bằng 1, nằm bên phải trục Oy.
Đúng 0
Bình luận (0)
Hãy biểu diễn các số phức z trên mặt phẳng tọa độ, biết left|zright|le2 và :
a) Phần thực của z không vượt quá phần ảo của nó
b) Phần ảo của z lớn hơn 1
c) Phần ảo của z nhỏ hơn 1, phần thực của z lớn hơn 1
Đọc tiếp
Hãy biểu diễn các số phức \(z\) trên mặt phẳng tọa độ, biết \(\left|z\right|\le2\) và :
a) Phần thực của \(z\) không vượt quá phần ảo của nó
b) Phần ảo của \(z\) lớn hơn 1
c) Phần ảo của \(z\) nhỏ hơn 1, phần thực của \(z\) lớn hơn 1
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện :
a) Phần thực của z bằng phần ảo của nó
b) Phần thực của z là số đối của phần ảo của nó
c) Phần ảo của z bằng hai lần phần thực của nó cộng với 1
d) Môđun của z bằng 1, phần thực của z không âm
Đọc tiếp
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện :
a) Phần thực của \(z\) bằng phần ảo của nó
b) Phần thực của \(z\) là số đối của phần ảo của nó
c) Phần ảo của \(z\) bằng hai lần phần thực của nó cộng với 1
d) Môđun của \(z\) bằng 1, phần thực của \(z\) không âm
Cho số phức z có phần ảo gấp hai phần thực và z + 1 = 2 5 5 . Khi đó mô đun của z là
A. 4
B. 6
C. 2 5
D. 5 5
Chọn D
Số phức z có dạng z = a + 2ai (a ∈ R)
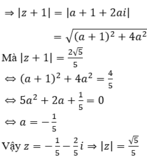
Đúng 0
Bình luận (0)
Tính tổng phần ảo các số phức z thỏa mãn |z| = 5 và phần thực của nó bằng 2 lần phần ảo.
A. 0
B. 1
C. 2
D.3
Chọn A.
Gọi số phức cần tìm là z = x = yi.
Ta có:
![]() hay x2 + y2 = 25 (*)
hay x2 + y2 = 25 (*)
Mặt khác: Số phức có phần thực của nó bằng 2 lần phần ảo nên x = 2y
thay vào phương trình (*) ta được: 5y2 = 25 hay ![]()
Vậy số phức cần tìm là: ![]()
Đúng 0
Bình luận (0)