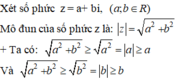
Vậy với mọi số phức thì phần thực và phần ảo của nó không vượt quá mô đun của nó.
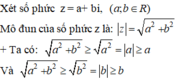
Vậy với mọi số phức thì phần thực và phần ảo của nó không vượt quá mô đun của nó.
Hãy biểu diễn các số phức z trên mặt phẳng tọa độ, biết |z| ≤ 2 và:
a) Phần thực của z không vượt quá phần ảo của nó;
b) Phần ảo của z lớn hơn 1;
c) Phần ảo của z nhỏ hơn 1, phần thực của z lớn hơn 1.
Hãy biểu diễn các số phức z trên mặt phẳng tọa độ, biết |z| ≤ 2 và: Phần thực của z không vượt quá phần ảo của nó
Thế nào là phần thực phần ảo, mô đun của một số phức? Viết công thức tính mô đun của số phức theo phần thực phần ảo của nó?
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bằng phần ảo của nó ;
b) Phần thực của z là số đối của phần ảo của nó ;
c) Phần ảo của z bằng hai lần phần thực của nó cộng với 1;
d) Modun của z bằng 1, phần thực của z không âm.
Cho số phức z có phần ảo gấp hai phần thực và z + 1 = 2 5 5 . Khi đó mô đun của z là
A. 4
B. 6
C. 2 5
D. 5 5
Tính tổng phần ảo các số phức z thỏa mãn |z| = 5 và phần thực của nó bằng 2 lần phần ảo.
A. 0
B. 1
C. 2
D.3
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện: Phần ảo của z bằng hai lần phần thực của nó cộng với 1
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện: Phần thực của z bằng phần ảo của nó
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện: Phần thực của z là số đối của phần ảo của nó